C51算法的缺陷
C51算法中虽然证明了\(\mathcal{T}\)Bellman算子在使用分布时是满足\(\gamma -contraction\)条件的,但是由于实际上无法在使用Wasserstein距离的时候用随机梯度下降进行优化,所以最后作者还是使用KL散度启发式的进行距离衡量。这与作者的原意相违背。QR-DQN算法就对这一过程进行了改进。
Wasserstein距离
Wasserstein距离简单来说就是用来衡量两个分布之间距离的指标。它能够衡量任意分布之间的距离,即使是离散分布与连续分布之间的距离也可以。相比于KL散度,Wasserstein距离不仅具有对称性,而且能够以更符合直观感受的方式衡量距离。
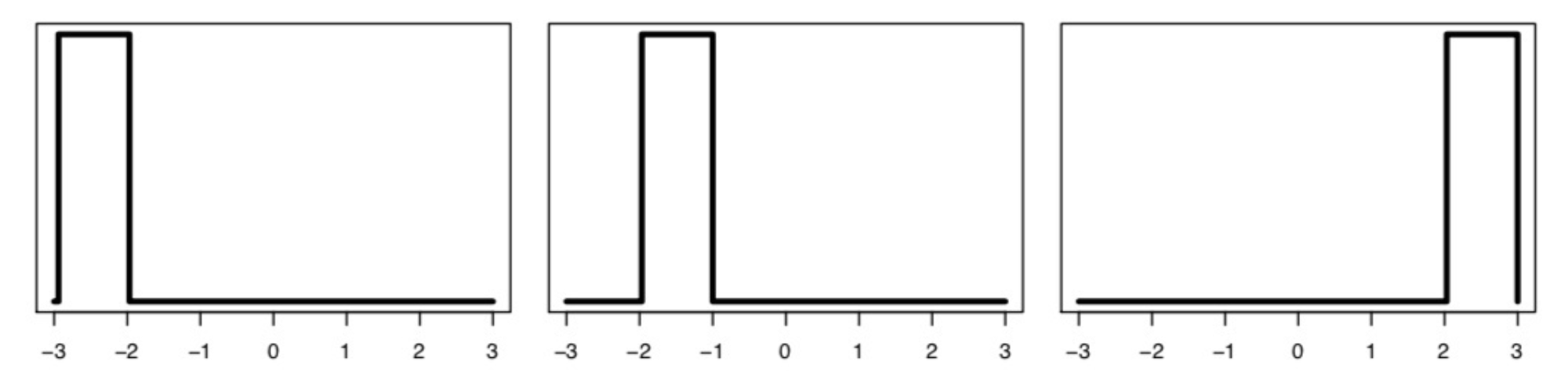
如在上图的情况下,可以看出相比于右端的分布,左端的分布与中间的分布之间的距离实际上要更近。因此从直观上来说,左端与中间的分布之间的距离应该要小于左端分布与右端分布之间的距离。但是在KL散度中,两个不重合分布之间的距离为固定的正无穷,因此无法应付这种情况。但是Wasserstein距离则能够反映上述区别。
Wasserstein距离的直观解释可以看这篇文章。Wasserstein距离的一般方程为:
\[ W _ { p } ( \mu , \nu ) : = \left( \inf _ { \gamma \in \Gamma ( \mu , \nu ) } \int _ { M \times M } d ( x , y ) ^ { p } \mathrm {~d} \gamma ( x , y ) \right) ^ { 1 / p } \]
其中\(\mu, \nu\)为两个随机变量,\(x,y\)分别为\(\mu, \nu\)两个分布下的任意取值,\(d(x,y)^p\)表示\(x,y\)之间的距离,\(p\)为级数。\(\gamma(x,y)\)表示\(\mu, \nu\)的任意联合分布,其存在于\(\Gamma ( \mu , \nu )\)这一空间中。根据这篇文章,Wasserstein距离可以被形象化为一个搬运石头的过程,而任意一个联合分布\(\gamma(x,y)\)则可以表示为一种搬运计划,\(d(x,y)\)表示为任意搬运起点与终点之间的距离。通过形象化的表达我们可以理解到,Wasserstein距离计算的是一种最优计划(从下确界\(\inf\)上可以看出来),这种计划能够通过挖土填土的方式把分布\(\mu\)转换成分布\(\nu\)。计划的优劣与搬运起点和终点之间的距离有关,搬运的距离越长,计划就越差。
如果\(\mu,\nu\)为一维分布,则Wasserstein距离可以简略为:
\[ W _ { p } ( U , Y ) = \left( \int _ { 0 } ^ { 1 } \left| F _ { Y } ^ { - 1 } ( \omega ) - F _ { U } ^ { - 1 } ( \omega ) \right| ^ { p } d \omega \right) ^ { 1 / p } \]
其中\(U,Y\)为两个分布,\(F _ { Y } ( y ) = \operatorname { Pr } ( Y \leq y )\)为分布\(Y\)的概率分布函数,其接收由\(Y\)分布采样的一个值\(y\),并给出这个分布下随机采样另一个值小于\(y\)的概率。而\(F _ { Y } ^ { - 1 } ( \omega ) : = \inf \left\{ y \in \mathbb { R } : \omega \leq F _ { Y } ( y ) \right\}\)为概率分布函数的反函数,其接收一个概率(或者分位点),返回这个分位点对应的\(y\)值。\(p\)同样表示为级数,当\(p=1\)时,这个公式就退化为实际上的搬运石头的距离。\(W_p(U,Y)\)的表达式,则是将这个分位点\(\omega\)从0到1进行积分。下图形象的描述了\(p=1\)情况下的Wasserstein距离。
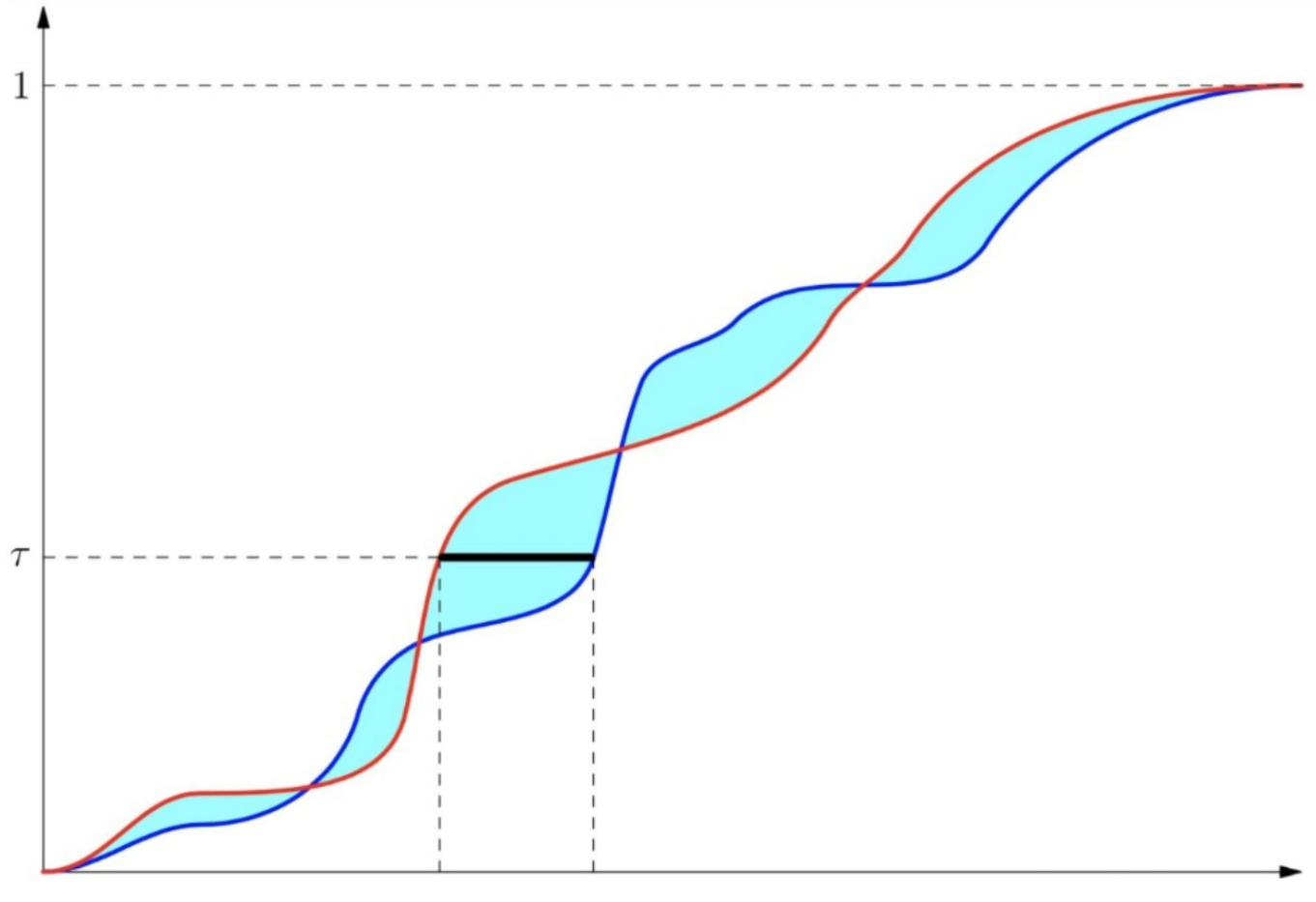
上图的红线和蓝线分别为\(P_X,P_Y\)的概率分布函数,横轴为随机变量的值,纵轴为累积概率。对于某一个概率(分位点)\(\tau\),我们可以计算得到两个值,分别为\(F^{-1}_{X}(\tau)\)以及\(F^{-1}_{Y}(\tau)\)。它们差值的绝对值就是上图中黑线的长度。把这个长度对各个分位点进行积分,就代表了两个分布的分布函数之间的差异。
同时对于Wasserstein距离,有几条特性。令\(d_{p}(U,V)\)为分布\(U,V\)之间的Wasserstein距离,\(a\)为一个标量,\(A\)为另一个分布。则有:
\[ \begin{aligned} d _ { p } ( a U , a V ) & \leq | a | d _ { p } ( U , V ) \\ d _ { p } ( A + U , A + V ) & \leq d _ { p } ( U , V ) \\ d _ { p } ( A U , A V ) & \leq \| A \| _ { p } d _ { p } ( U , V ) \end{aligned} \]
两个问题的说明
既然介绍了Wasserstein距离,那么以下针对两个问题进行说明。第一个问题是,为什么C51算法中不能使用随机梯度下降优化作为loss的Wasserstein距离?第二个问题是,分布式的Bellman算子是否满足\(\gamma - contraction\)条件?
我们先就第一个问题进行说明。我们令\(\{P_{i}\}\)为随机变量的集合,其中\(I \in \mathbb{N}\)是指示标量。那么\(P=P_I\)是一个混合变量(\(P\)本身为随机变量集合,下标\(I\)又是随机的),并且所有的随机变量都与\(Q\)独立。令\(A _ { i } = \mathbb { I } [ I = i]\)(值可以为小数),则有:
\[ \begin{aligned} d _ { p } ( P , Q ) & = d _ { p } \left( P _ { I } , Q \right) \\ & = d _ { p } \left( \sum _ { i } A _ { i } P _ { i } , \sum _ { i } A _ { i } Q \right) \\ & \leq \sum _ { i } d _ { p } \left( A _ { i } P _ { i } , A _ { i } Q \right) \\ & \leq \sum _ { i } \operatorname { Pr } \{ I = i \} d _ { p } \left( P _ { i } , Q \right) \\ & = \mathbb { E } _ { I } d _ { P } \left( P _ { i } , Q \right) \end{aligned} \]
其中第三行到第四行的转化利用了Wasserstein距离的特性3。第二行到第三行的证明其实利用了距离不会为负数的特性。我们假设\(P_1 \sim N \left( -1, \sigma 1 ^ { 2 } \right)\),\(P_2 \sim N \left( 1, \sigma 2 ^ { 2 } \right)\),\(Q \sim N \left( 0, \sigma 3 ^ { 2 } \right)\),且\(A_1=A_2=0.5\),\(1/4\sigma 1 ^ { 2 } + 1/4 \sigma 2 ^ { 2 } = \sigma 3 ^ { 2 }\)。可以看出,\(d_p(0.5P_1, 0.5Q), d_p(0.5P_1, 0.5Q)\)的距离都是大于0的,但是\(\sum _ { i } A _ { i } P _ { i } = 0.5P_1 + 0.5P_2 = Q\),而\(d_p(Q,Q)\)则是等于0的。因为距离不会为负数,所以先把分布相加之后计算得到的距离肯定比分开计算得到的距离要短。
因为有:
\[ d _ { p } ( P , Q ) \leq \mathbb { E } _ { I } d _ { P } \left( P _ { i } , Q \right) \]
所以有:
\[ \nabla _ { Q } d _ { p } \left( P _ { I } , Q \right) \neq \nabla _ { Q } \mathbb { E } _ { I } d _ { P } \left( P _ { i } , Q \right) \]
因此无法直接使用随机梯度下降优化Wasserstein距离构成的loss。
现在就第二个问题进行说明。如果要证明分布式的Bellman算子满足\(\gamma -contraction\)条件,我们需要证明:
\[ \begin{aligned} \bar { d } _ { p } \left( \mathcal { T } ^ { \pi } Z _ { 1 } , \mathcal { T } ^ { \pi } Z _ { 2 } \right) \leq \gamma \bar { d } _ { p } \left( Z _ { 1 } , Z _ { 2 } \right) \end{aligned} \]
其中\(\bar { d } _ { p } \left( Z _ { 1 } , Z _ { 2 } \right) : = \sup _ { x , a } W _ { p } \left( Z _ { 1 } ( x , a ) , Z _ { 2 } ( x , a ) \right)\),对于\(\bar { d } _ { p } \left( \mathcal { T } ^ { \pi } Z _ { 1 } , \mathcal { T } ^ { \pi } Z _ { 2 } \right)\)也是一样。这里取上确界的原因是\(\gamma - contraction\)需要使用无穷级数,而无穷级数就相当于\(\max\),也就是相当于取上确界。因为:
\[ \begin{array} { c } \bar { d } _ { p } \left( \mathcal { T } ^ { \pi } Z _ { 1 } , \mathcal { T } ^ { \pi } Z _ { 2 } \right) = \sup _ { x , a } d _ { p } \left( \mathcal { T } ^ { \pi } Z _ { 1 } ( x , a ) , \mathcal { T } ^ { \pi } Z _ { 2 } ( x , a ) \right) \end{array} \]
而且有:
\[ \\ d _ { p } \left( \mathcal { T } ^ { \pi } Z _ { 1 } ( x , a ) , \mathcal { T } ^ { \pi } Z _ { 2 } ( x , a ) \right) = d _ { p } \left( R ( x , a ) + \gamma P ^ { \pi } Z _ { 1 } ( x , a ) , R ( x , a ) + \gamma P ^ { \pi } Z _ { 2 } ( x , a ) \right) \\ \leq \gamma d _ { p } \left( P ^ { \pi } Z _ { 1 } ( x , a ) , P ^ { \pi } Z _ { 2 } ( x , a ) \right) \\ \leq \gamma \sup _ { x ^ { \prime } , a ^ { \prime } } d _ { p } \left( Z _ { 1 } \left( x ^ { \prime } , a ^ { \prime } \right) , Z _ { 2 } \left( x ^ { \prime } , a ^ { \prime } \right) \right) \]
第一行到第二行利用了Wasserstein距离的特性1,2,第三行是因为有\(P ^ { \pi } Z _ { 1 } ( x , a ) = Z_1(x',a')\),因为上确界的性质所以成立。
结合上述2式,有:
\[ \begin{aligned} \bar { d } _ { p } \left( \mathcal { T } ^ { \pi } Z _ { 1 } , \mathcal { T } ^ { \pi } Z _ { 2 } \right) & = \sup _ { x , a } d _ { p } \left( \mathcal { T } ^ { \pi } Z _ { 1 } ( x , a ) , \mathcal { T } ^ { \pi } Z _ { 2 } ( x , a ) \right) \\ & \leq \gamma \sup _ { x ^ { \prime } , a ^ { \prime } } d _ { p } \left( Z _ { 1 } \left( x ^ { \prime } , a ^ { \prime } \right) , Z _ { 2 } \left( x ^ { \prime } , a ^ { \prime } \right) \right) \\ & = \gamma \bar { d } _ { p } \left( Z _ { 1 } , Z _ { 2 } \right) \end{aligned} \]
所以能够满足\(\gamma - contraction\)条件。
近似最小化Wasserstein距离
根据前面对两个问题的说明,我们知道无法直接使用Wasserstein距离进行梯度下降优化,因此QR-DQN算法使用了近似方法。根据Wasserstein距离一节的说明可以知道,当在一维分布且\(p=1\)的情况下,Wasserstein距离其实就相当于两个分布的分布函数之间相差的面积。因此QR-DQN算法放弃考虑概率密度函数,而转向考虑概率分布函数。它通过锁定概率分布函数上各个指定分位点的值来概括这个分布,并使用分位数回归的方法来进行拟合。
在C51算法中,我们使用\(N\)个atoms\(\{z_0, z_1, \cdots , z_{N-1}\}\)作为基准,再用\(N\)个离散的分布\(\{p_0, p_1, \cdots, p_{N-1}\}\)来描述这个分布。这种形式不太适合Wasserstein距离,但是我们可以使用相似的方法。
我们可以把概率分布函数的\(y\)轴均等的分成\(N\)等分,例如下面分成了10等分:(图源这里)

我们取10个区间的中点作为记录点,得到10个分位数。可以表示为:
\[ \hat { \tau } _ { i } = \frac { 2 ( i - 1 ) + 1 } { 2 N } , \quad i = 1 , \ldots , N \]
使用中点作为记录点是有原因的,具体可以看这篇文章的3.3部分。
使用概率密度函数来可视化的话就像这样:
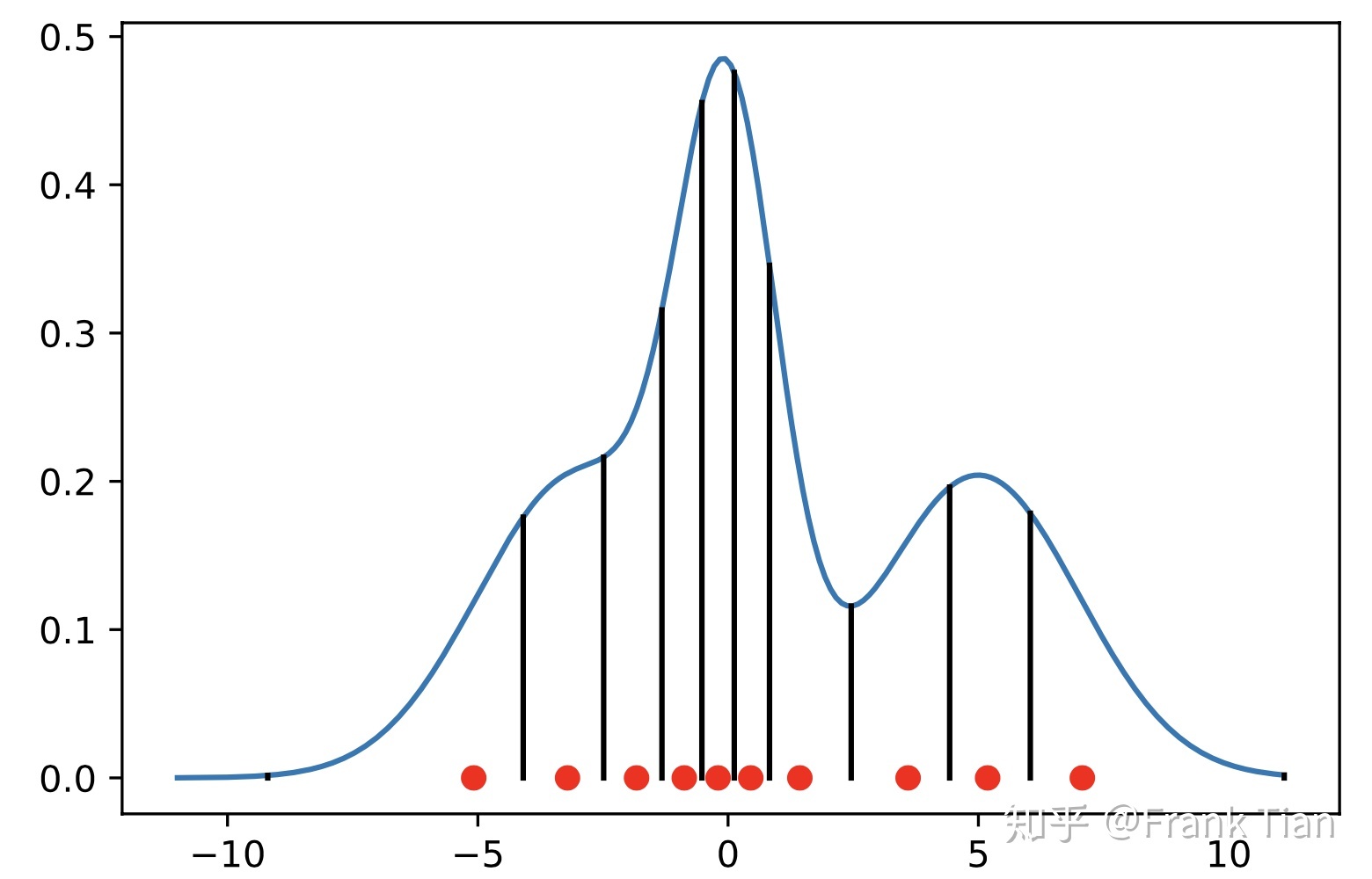
分位数回归
具体可以参照这篇文章。
在传统的回归中,对于自变量\(x\),我们想要建立方程\(\mu(x,\beta)\)拟合因变量\(y\)的期望,我们使用的损失函数为:
\[ L _ { M S E } = \min _ { \beta } \sum _ { i } ^ { n } \left( y _ { i } - \mu \left( x _ { i } , \beta \right) \right) ^ { 2 } \]
但如果我们想求\(y\)的中位数,那我们就应该把损失函数换成:
\[ L _ { M A E } = \sum _ { i } ^ { n } \left| y _ { i } - \xi \left( x _ { i } , \beta \right) \right| \]
或者写成:
\[ L _ { M A E } = \sum _ { i : y _ { i } \geq \xi \left( x _ { i } , \beta \right) } \left( y _ { i } - \xi \left( x _ { i } , \beta _ { \tau } \right) \right) + \sum _ { i : y _ { i } < \xi \left( x _ { i } , \beta \right) } \left( \xi \left( x _ { i } , \beta \right) - y _ { i } \right) \]
至于为什么,因为这个函数当\(\xi (x _ { i } , \beta ) \)预测为中位数时导数等于0,导数为:
\[ \begin{array} { l } \nabla _ { \beta } L _ { M A E } = \sum _ { i } ^ { n } \nabla _ { i } \\ \nabla _ { i } = \left\{ \begin{array} { l l } 1 & i : y _ { i } < \xi \left( x _ { i } , \beta \right) \\ - 1 & i : y _ { i } \geq \xi \left( x _ { i } , \beta \right) \end{array} \right. \end{array} \]
对于其他分位数,我们可以给损失函数的两项分配不同的权重,假设我们要求\(\tau\)分位数,则损失函数可以写为:
\[ L _ { \tau } = \sum _ { i : y _ { i } \geq \xi \left( x _ { i } , \beta _ { \tau } \right) } \tau \left( y _ { i } - \xi \left( x _ { i } , \beta _ { \tau } \right) \right) + \sum _ { i : y _ { i } < \xi \left( x _ { i } , \beta _ { \tau } \right) } ( 1 - \tau ) \left( \xi \left( x _ { i } , \beta _ { \tau } \right) - y _ { i } \right) \]
简单描述就是给\(\tau\)分位数左边的样本分配\((1-\tau)\)的权重,对右边的样本分配\(\tau\)的权重。这样当导数为0的时候方程刚好能够正确预测\(\tau\)分位数的值。这个时候的导数可以表示为:
\[ \begin{array} { l } \nabla _ { \beta } L _ { \tau } = \sum _ { i } ^ { n } \nabla _ { i } \\ \nabla _ { i } = \left\{ \begin{array} { l l } 1 - \tau & i : y _ { i } < \xi \left( x _ { i } , \beta _ { \tau } \right) \\ - \tau & i : y _ { i } \geq \xi \left( x _ { i } , \beta _ { \tau } \right) \end{array} \right. \end{array} \]
我们还可以换一种形式表示\(L_\tau\),令\(\delta_{\text{statement}}\)表示:
\[ \delta _ { \text {statement } } = \left\{ \begin{array} { l l } 1 & \text { statement is ture } \\ 0 & \text { otherwise } \end{array} \right. \]
于是有:
\[ \left| \tau - \delta _ { y _ { i } < \xi \left( x _ { i } , \beta \right) } \right| = \left\{ \begin{array} { l l } | \tau - 1 | = 1 - \tau & \text { if } y _ { i } < \xi \left( x _ { i } , \beta \right) \\ \tau & \text { if } y _ { i } \geq \xi \left( x _ { i } , \beta \right) \geq \theta \end{array} \right. \]
所以
\[ \begin{aligned} L _ { \tau } & = \mathbb { E } \left[ \left| y _ { i } - \xi \left( x _ { i } , \beta _ { \tau } \right) \right| \left| \tau - \delta _ { y _ { i } < \xi \left( x _ { i } , \beta \right) } \right| \right] \\ & = \mathbb { E } \left[ \rho _ { \tau } \left( y _ { i } - \xi \left( x _ { i } , \beta _ { \tau } \right) \right) \right] \end{aligned} \]
因为两个绝对值内的式子都在同时正同时负,所以抵消了。其中\(\rho_{\tau}(u) = u(\tau - \delta_{u <0})\)。
因为绝对值\(|u|\)在0处不可导,所以论文中使用的是近似的函数:
\[ \mathcal { L } _ { \kappa } ( u ) = \left\{ \begin{array} { l l } \frac { 1 } { 2 } u ^ { 2 } & \text { if } | u | \leq \kappa \\ \kappa \left( | u | - \frac { 1 } { 2 } \kappa \right) & \text { otherwise } \end{array} \right. \]
其中\(\kappa\)也是超参数,一般取1,这时的图像如下:
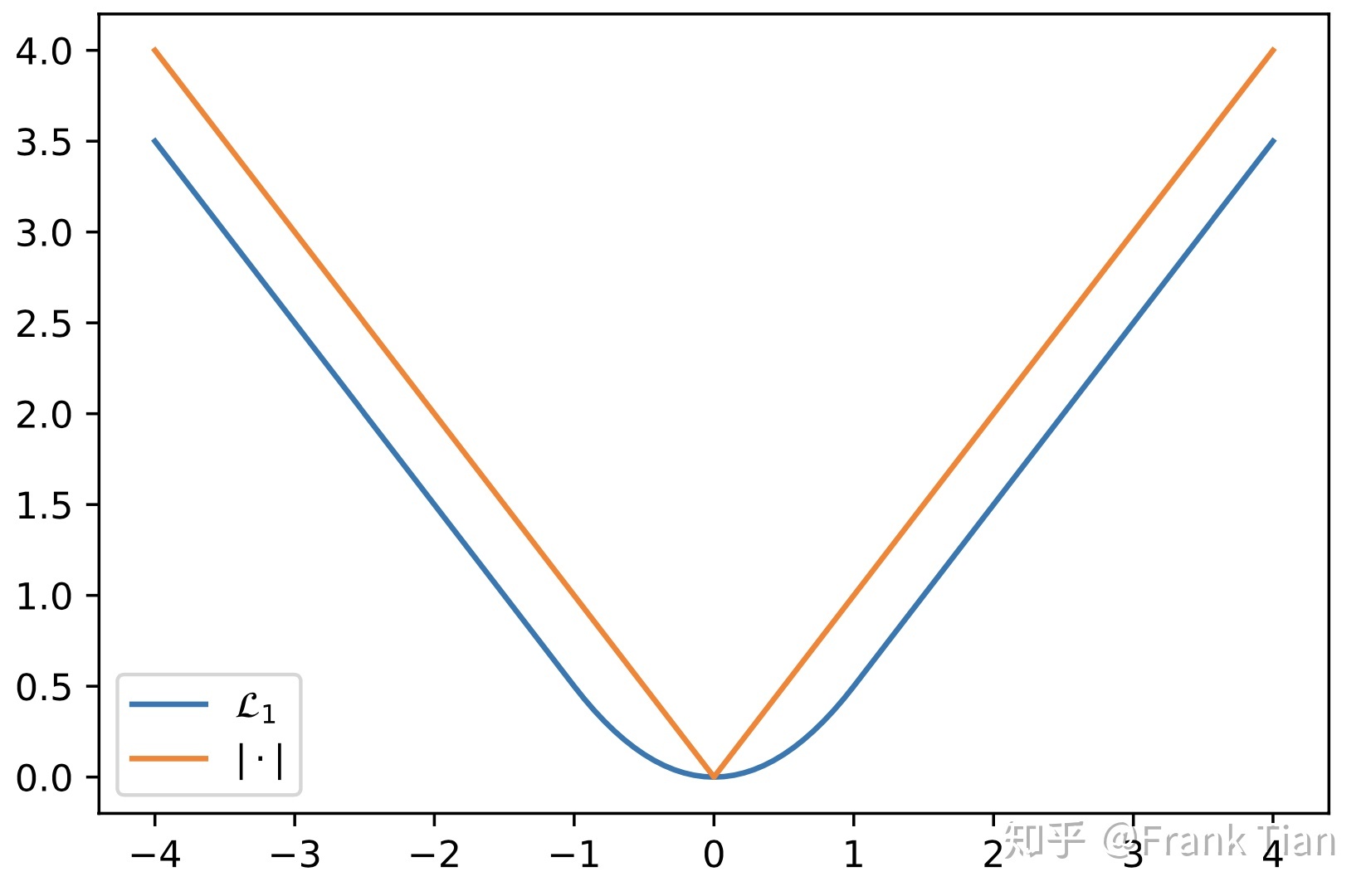
最终我们把损失函数定为\(\mathbb { E } \left[ \rho^{1} _ { \tau } \left( y _ { i } - \xi \left( x _ { i } , \beta _ { \tau } \right) \right) \right] \),其中\(\tau\)表示分位数,1表示\(\kappa\)的值。
其实使用分位数回归来近似Wasserstein距离的损失函数也是需要证明的,证明过程可以参照这篇文章的3.3部分。
训练过程
首先神经网络接收状态\(s\),并输出\(|\mathcal{A}| \times N\)的矩阵,其中每一行\(\{\theta_0, \theta_1, \cdots, \theta_{N-1}\}\)表示各个分位数对应的\(Q(s,a)\)值。
同样是使用类q-learning的思想。采样一个\((s,a,r,s')\),接下来我们需要计算出\(a^*\),一样用\(Q(s,a)\)来计算。有:
\[ Q(s',a') = \sum_{j}q_j \theta_j(x',a') \]
其中\(q_j = 1/N\)。根据\(Q(s',a')\)挑出最大的\(a^*\),设其分布为\(\{\theta'_0, \theta'_1, \cdots, \theta'_{N-1}\}\),那么目标分布表示为:
\[ \mathcal { T } \theta _ { j } ^ { \prime } = r + \gamma \theta _ { j } ^ { \prime } , \quad i = 0 , \ldots , N - 1 \]
所以现在有当前分布\(Z(s,a) = \{\theta_0, \theta_1, \cdots, \theta_{N-1}\}\),目标分布\(\{r+\gamma\theta'_0, r+\gamma\theta'_1, \cdots, r+\gamma\theta'_{N-1}\}\),使用损失函数\(L_\tau = \mathbb { E } \left[ \rho _ { \tau } \left( y _ { i } - \xi \left( x _ { i } , \beta _ { \tau } \right) \right) \right]\)计算loss有:
\[ \begin{aligned} L _ { \beta } & = \sum _ { i = 1 } ^ { N } \mathbb { E } _ { Y } \left[ \rho _ { \tau _ { i } } ^ { 1 } \left( Y - \xi ( \beta ) _ { i } \right) \right] \\ & = \sum _ { i = 1 } ^ { N } \mathbb { E } _ { \mathcal { T } Z ^ { \prime } } \left[ \rho _ { \hat { \tau } _ { i } } ^ { 1 } \left( \mathcal { T } Z ^ { \prime } - \theta _ { i } \right) \right] \\ & = \frac { 1 } { N } \sum _ { i = 1 } ^ { N } \sum _ { j = 1 } ^ { N } \left[ \rho _ { \hat { \tau } _ { i } } ^ { 1 } \left( \mathcal { T } \theta _ { j } ^ { \prime } - \theta _ { i } \right) \right] \end{aligned} \]
注意每一个\(\theta_j\)都要与所有的\(r+\gamma\theta'_i\)计算loss(根据分位数回归方程,不需要对\(y\)进行筛选),因此需要计算两次求和。上式中,有:
\[ \mathcal{T}Z' = r + \gamma Z(x',a^*) \]
且\(\hat { \tau } _ { i }\)就是用来决定\(N\)个分位数的值:
\[ \hat { \tau } _ { i } = \frac { 2 i + 1 } { 2 N } , \quad i = 0 , \ldots , N - 1 \]
最后算法如下:

