经典强化学习与值分布强化学习的区别
由于状态转移的随机性,状态表示的混叠效应(编码状态时带来的信息丢失)以及函数逼近的引入(使用函数表示状态价值带来的信息丢失),状态价值通常具有一定随机性,并可以用某种分布来表示。经典强化学习(DQN算法等)使用单个值的形式预测状态价值可能会忽略掉许多有效信息。因此值分布强化学习旨在拟合出状态价值的分布,从而提高预测准确性。值得一提的是,PG类算法在应用于连续动作时通常也会以某种分布作为输出。但这种情况下输出的分布为动作的概率分布,主体为动作;而值分布强化学习输出的分布为给定状态-动作对情况下其动作价值的分布,主体为价值。
Bellman算子
算子,即operator,接受函数输入,并输出函数。若\(Q(s,a)\)是一个函数,如果\(s\)是一个\(n\)维的变量,\(a\)是一个\(m\)维的变量,那么动作价值函数\(Q\)是一个\(\mathbb{R}^n \times \mathbb{R}^m \rightarrow \mathbb{R}\)的函数。我们可以引入Bellman算子\(\mathcal{T}\)来表示Bellman方程。对于某一个具体策略\(\pi\)以及状态转移矩阵\(P\),我们有:
\[ \mathcal { T } ^ { \pi } Q ( x , a ) : = \mathbb { E } R ( x , a ) + \gamma \underset { P , \pi } { \mathbb { E } Q } \left( x ^ { \prime } , a ^ { \prime } \right) \]
其中\(R(s,a)\)是环境的一部分,其输入输出与\(Q\)相同,为\(\mathbb{R}^n \times \mathbb{R}^m \rightarrow \mathbb{R}\)。可以看出,Bellman算子接收输入函数\(Q\),并输出函数\(Q'\)。
从Bellman算子的角度来描述策略评估,其实就是在找一个函数\(Q\),满足\(\mathcal{T}^\pi Q = Q\),也就是在找算子的不动点(经过算子运算后函数不发生改变)。具体可以参考这一篇文章。
以相同的手法我们可以定义最优Bellman算子,其用来表示Bellman最优方程:
\[ \mathcal { T } Q ( x , a ) : = \mathbb { E } R ( x , a ) + \gamma \mathbb { E } _ { P } \max _ { a ^ { \prime } \in \mathcal { A } } Q \left( x ^ { \prime } , a ^ { \prime } \right) \]
同样的,使用最优Bellman算子做策略评估,就是在找算子\( \mathcal{T}\)的不动点。
同样由这篇文章,可以证明算子\(\mathcal{T}, \mathcal{T}^\pi\)都满足\(\gamma -contraction\)的条件,即有:
\[ \left\| \mathcal{T}^\pi Q_1 - \mathcal{T}^\pi Q_2 \right\| _ { \infty } \leq \gamma \left\| Q_1 - Q_2 \right\| _ { \infty } \\ \]
\[ \left\| \mathcal{T} Q_1 - \mathcal{T} Q_2 \right\| _ { \infty } \leq \gamma \left\| Q_1 - Q_2 \right\| _ { \infty } \]
于是根据Contraction Mapping Theorem,上述两个算子都具有唯一的不动点。即有:
\[ \begin{array} { l } \mathcal { T } ^ { \pi \infty } Q = Q ^ { \pi } \\ \mathcal { T } ^ { \infty } Q = Q ^ { * } \end{array} \]
KL散度
对于分布\(p,q\),它们的KL散度定义为:
\[ \mathrm { KL } ( p \| q ) = \int p ( x ) \log \frac { p ( x ) } { q ( x ) } d x \]
KL散度能衡量两个分布之间的差异,但是不具有对称性。其可以用于离散形式的计算,有:
\[ \mathrm { KL } ( p \| q ) = \sum _ { i = 1 } ^ { N } p \left( x _ { i } \right) \log \frac { p \left( x _ { i } \right) } { q \left( x _ { i } \right) } = \sum _ { i = 1 } ^ { N } p \left( x _ { i } \right) \left[ \log p \left( x _ { i } \right) - \log q \left( x _ { i } \right) \right] \]
Distributional DQN
Distributional DQN将传统DQN中的value function换成了value distribution。原来的DQN中的值函数为\(Q(s,a)\),它接收一个状态动作对\(s,a\),并输出实数格式的动作价值\(Q\)。
与其相对,Distributional DQN接收一个状态动作对\(x,a\),并输出一个值分布\(Z(x,a)=P(v | x,a)\),这个分布描绘了状态动作对\(x,a\)所有可能的价值\(v\)的范围以及可能性。易得,\(Q(x,a) = \mathbb{E}[Z(x,a)]\)。
针对值分布,可以定义状态转移算子:
\[ \begin{aligned} P ^ { \pi } Z ( x , a ) & : = Z \left( X ^ { \prime } , A ^ { \prime } \right) \\ X ^ { \prime } & \sim P ( \cdot \mid x , a ) , A ^ { \prime } \sim \pi \left( \cdot \mid X ^ { \prime } \right) \end{aligned} \]
这个算子是\(\mathcal { Z } \rightarrow \mathcal { Z }\),也就是接收一个分布,并输出另一个分布。可以看出,算子接收当前状态动作对\(x,a\)生成的值分布\(Z(x,a)\),根据状态转移矩阵\(P\)以及当前策略\(\pi\)生成下一时刻状态动作对\(x',a'\)生成的值分布\(Z(x',a')\)。
在值分布情况下的Bellman算子就可以被定义为:
\[ \mathcal { T } ^ { \pi } Z ( x , a ) : \stackrel { D } { = } R ( x , a ) + \gamma P ^ { \pi } Z ( x , a ) \]
与状态转移算子\(P^\pi\)相同,值分布下的Bellman算子同样也是\(\mathcal{Z} \rightarrow \mathcal{Z}\)。可视化后的情况如下图:
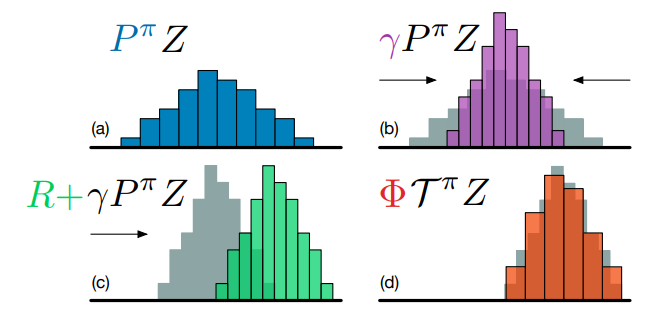
在DQN中,我们计算出一个\(r + \gamma \underset{a^*} \max Q(x', a^*)\),并使当前\(Q(x,a)\)尽量靠近这个值。相对应的,我们可以在Distributional DQN中定义最优Bellman算子\(\mathcal{T} Z\),其满足:
\[ \mathcal { T } Z = \mathcal { T } ^ { \pi } Z \text { for } \pi \in \mathcal { G } _ { Z } \\ \mathcal { G } _ { Z } : = \left\{ \pi : \sum _ { a } \pi ( a \mid x ) \mathbb { E } Z ( x , a ) = \max _ { a ^ { \prime } \in \mathcal { A } } \mathbb { E } Z \left( x , a ^ { \prime } \right) \right\} \]
\(\mathcal { G } _ { Z }\)看起来很复杂,但实际上指的是令策略\(\pi\)取最优策略。因此,在Distributional DQN中,我们需要让当前值分布\(Z(x,a)\)尽可能的靠近\(\mathcal{T} Z(x,a)\)这个分布。
C51定义
由于\(Z(x,a)\)分布并不一定符合某种特殊的预设模式,因此C51方法放弃使用高斯分布等参数化方式表示\(Z(x,a)\),而是使用了51个等间距的atoms描绘一个分布。实际上其与描绘分布的直方图差距不大,但是直方图更注重区间,而C51算法使用的comb form的方法更注重"点"。当然这个分布肯定是近似的结果,点的范围和个数取决于应用情况。实际上,假设分布\(Z(x,a)\)的上界为\(V_{MAX}\),下界\(V_{MIN}\),将最大值和最小值之间的区间均匀化为\(N\)个点,则每个点\(\mathcal{z}_i\)有:
\[ \left\{ z _ { i } = V _ { \min } + i \Delta z : 0 \leq i < N , \Delta z : = \frac { V _ { M A X } - V _ { M I N } } { N - 1 } \right\} \]
例如,当\(N=7\)时,一共有7个atoms,其分布可能为:
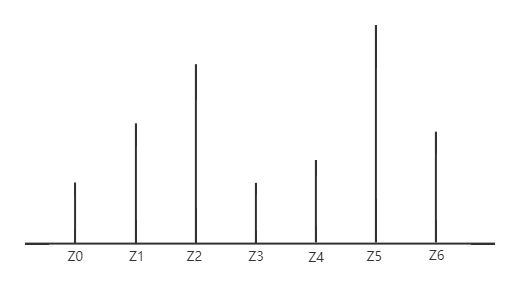
现在我们来考虑C51的网络架构。在DQN中,网络的输入为\(s\),输出为\(|\mathcal{A}|\)维的一个向量\((Q(s,a_1), Q(s,a_2),...,Q(s,a_m))\)。向量的每一个元素代表对应动作状态对\(s,a\)的预测\(Q\)值。而在C51算法中,输出变成了一个矩阵。矩阵的行数为\(|\mathcal{A}|\),每一行代表给定\(s,a\)的值分布。矩阵的列数为\(N\),每一列代表值分布在给定atom上的概率。若atoms集合为\(\left\{ z _ { 0 } , z _ { 1 } , \cdots , z _ { N - 1 } \right\}\),C51的输出应该为\((\left\{ p _ { 0 } ^ { a_1 } , p _ { 1 } ^ { a_1 } , \cdots , p _ { N - 1 } ^ { a_1 } \right\}, \left\{ p _ { 0 } ^ { a_2 } , p _ { 1 } ^ { a_2 } , \cdots , p _ { N - 1 } ^ { a_2 } \right\} \cdots , \left\{ p _ { 0 } ^ { a_m } , p _ { 1 } ^ { a_m } , \cdots , p _ { N - 1 } ^ { a_m } \right\})\)。
为了保证神经网络输出的矩阵的每一行构成一个离散的分布,可以对神经网络的输出进行softmax操作。具体为:
\[ Z _ { \theta } ( x , a ) = z _ { i } \quad w . p . p _ { i } ( x , a ) : = \frac { e ^ { \theta _ { i } ( x , a ) } } { \sum _ { j } e ^ { \theta _ { j } ( x , a ) } } \]
C51损失函数
网络结构定义完成后,我们需要设置损失函数,从而完成训练过程。在DQN中,由于网络输出为一个实数,因此我们可以使用均方误差作为损失函数。但是C51算法输出为一个分布,因此我们需要找到一个衡量分布之间距离的方法。通常我们使用Wasserstein Metric作为衡量分布距离的方法(具体解释看这篇文章,其实也看不太懂呜呜)。使用Wasserstein Metric可以保证Bellman算子在输出分布的情况下也满足\(\gamma - contraction\)的条件。但是,对于Q-learning实际用到的最优Bellman算子则没有这样的理论保证。而且使用SGD方法训练时是没有办法保持Wasserstein Metric的。因此,C51算法使用了KL散度启发式的衡量两个分布的距离。
投影Bellman更新
使用KL散度的离散形式计算可以很容易的算出两个分布之间的距离。但是在实际运算中还会产生一个问题。我们可以通过模拟整个过程找出问题。
首先我们从Buffer中采样一个\((s,a,r,s')\),根据q-learning函数使用的最优Bellman算子,有:
\[ \mathcal { T } Z ( x , a ) : \stackrel { D } { = } R ( x , a ) + \gamma P Z ( x , a ) \]
因此为了改善\(Z(x,a)\),我们需要计算\(R(x,a) + \gamma Z(x',a^*)\)。在DQN中,\(a^*\)的选择是根据\(a ^ { * } \leftarrow \arg \max _ { a } Q \left( x' , a \right)\)标准的。在C51中我们沿用这个标准,并通过\(Q(x,a) = \mathbb{E}[Z(x,a)]\)来计算\(Q(x,a)\)。具体有:
\[ Q \left( s _ { t + 1 } , a \right) : = \sum _ { i } z _ { i } p _ { i } \left( s _ { t + 1 } , a \right) \]
根据上述标准,我们可以从target network中获得\(Z(x',a^*)\)的结果,是一个\(N\)维的向量,我们设其为\(p'\)。那么\(R(x,a) + \gamma Z(x',a^*)\)分布就可以表示为:
有\(p'_{0}\)的概率取\(R + \gamma z_0\)
有\(p'_{1}\)的概率取\(R + \gamma z_1\)
......
有\(p'_{N-1}\)的概率取\(R + \gamma z_{N-1}\)
但我们检查\(Z(x,a)\)可以发现,其可以表示为:
有\(p'_{0}\)的概率取\( z_0 \)
有\(p'_{1}\)的概率取\(z_1\)
......
有\(p'_{N-1}\)的概率取\(z_{N-1}\)
可以发现,\(Z(x,a)\)与\(R(x,a) + \gamma Z(x',a^*)\)的atoms没有对齐。C51的解决方法是,将\(R + \gamma z_k\)的概率分摊到\(z_k\)和\(z_{k+1}\)上。具体的分摊比例按照\(R + \gamma z_k\)到\(z_k\)与\(z_{k+1}\)的距离的反比即可。
以这篇文章中的例子,令\(\hat { \mathcal { T } } z _ { 0 } = R + \gamma z_0\)对应的概率为\(p_0(x',a')\),将其投影到相邻的支点\(z_0,z_1\)上,如图:
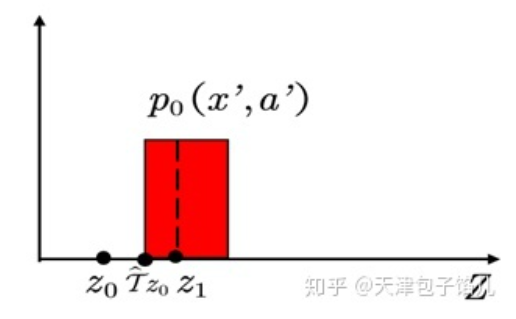
则\(z_0\)分得的概率的大小为:
\[ [1 - \frac { \hat { \mathcal { T } } z _ { 0 } - z _ { 0 } } { z_1 - z_0 }]p _ { 0 } \left( x ^ { \prime } , a ^ { \prime } \right) \]
经过上述分配,我们可以得到一个新的分布\(\Phi { \mathcal { T } } Z ( x , a )\),损失函数可得为:
\[ D_{KL}(\Phi { \mathcal { T } } Z ( x , a ) || Z(x,a)) \]
C51具体算法流程如下:

