样本分布
在相同的条件下,对总体\(X\)进行\(n\)次重复的,独立的观察,得到\(n\)个结果\((x_1,x_2,...,x_n)\),称\((x_1,x_2,...,x_n)\)为来自总体\(X\)的简单随机样本,其具有两条性质:
- \((x_1,x_2,...,x_n)\)与总体具有相同的分布
- \((x_1,x_2,...,x_n)\)之间相互独立
统计量与统计量的分布
统计量:不含未知参数的,随机样本\((x_1,x_2,...,x_n)\)的函数。统计量是一个随机变量,完全由样本所决定。统计量是进行统计推断的工具。
两个重要的统计量:
\[ \bar { x } = \frac { 1 } { n } \sum _ { i = 1 } ^ { n } x _ { i } \]
\[ s ^ { 2 } = \frac { \sum _ { i = 1 } ^ { n } \left( x _ { i } - \bar { x } \right) ^ { 2 } } { n - 1 } \]
统计量的分布被称为抽样分布。三个来正态分布的抽样分布为\(\chi ^ { 2 }\)分布,\(t\)分布,\(F\)分布,被称为统计学的三大分布。
设随机变量\(X\)服从\(N(0,1)\)分布,\(x_1,x_2,...,x_n\)为\(X\)的样本,则\(\chi^{2}\)统计量为
\[ \chi ^ { 2 } = \sum _ { i = 1 } ^ { n } x _ { i } ^ { 2 } \]
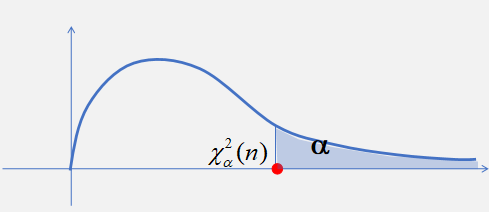
\(\chi ^ { 2 }\)分布的分位点:对于给定的正数\(\alpha\),有\(0 <\alpha < 1\),称满足条件
\[ P \left\{ \chi ^ { 2 } > \chi _ { \alpha } ^ { 2 } ( n ) \right\} = \int _ { \chi _ { \alpha } ^ { 2 } ( n ) } ^ { \infty } f ( y ) d y = \alpha \]
的点\(\chi _ { \alpha } ^ { 2 } ( n )\)为分布上的\(\alpha\)分位点。
自由度为\(n\)的\(t\)分布,记为\(t(n)\),是由\(N(0,1)\)以及\(\chi ^ { 2 }(n)\)分布组成的,表达式为
\[ T = \frac { X } { \sqrt { \frac { Y } { n } } } \]
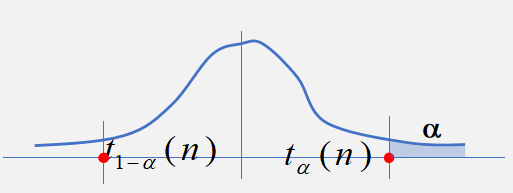
\(t\)分布的分位点:对于给定的正数\(\alpha\),有\(0 <\alpha < 1\),称满足条件
\[ P \left\{ t > t _ { \alpha } ( n ) \right\} = \int _ { t _ { \alpha } ( n ) } ^ { \infty } h ( t ) d t = \alpha \]
的点\(t _ { \alpha } ( n )\)为\(t(n)\)分布上的\(\alpha\)分位点。由分布的对称性可知,\(t_{1- \alpha}(n) = -t_{\alpha}(n)\)。
\(F\)分布是由两个\(\chi ^ { 2 }\)分布之比组成的
\[ F = \frac { \frac { U } { n } } { \frac { V } { m } } \]
其中\(U\)服从\(\chi ^ { 2 }(n)\),\(V\)服从\(\chi ^ { 2 }(m)\)。
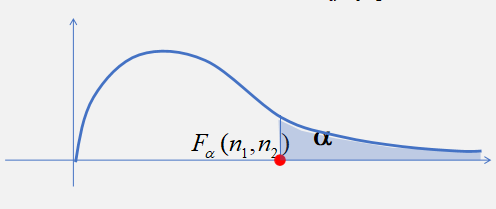
\(F\)分布的分位点:对于给定的正数\(\alpha\),有\(0 <\alpha < 1\),称满足条件
\[ P \left\{ F > F _ { \alpha } \left( n _ { 1 } , n _ { 2 } \right) \right\} = \int _ { F _ { \alpha } \left( n _ { 1 } , n _ { 2 } \right) } ^ { \infty } \varphi ( y ) d y = \alpha \]
若\(x_1,x_2,...,x_n\)是一般正态分布\(N(\mu,\sigma^2)\)的一个随机样本,则样本均值函数与样本方差函数满足如下的性质:
\[ \frac { \bar { X } - \mu } { \frac { \delta } { \sqrt { n } } } \sim N ( 0,1 ) \]
\[ \frac { ( n - 1 ) S ^ { 2 } } { \delta ^ { 2 } } \sim \chi ^ { 2 } ( n - 1 ) \]
\[ \frac { \bar { X } - \mu } { \frac { S } { \sqrt { n } } } \sim t ( n - 1 ) \]
\[ \frac { S _ { 1 } ^ { 2 } / \sigma _ { 1 } ^ { 2 } } { S _ { 2 } ^ { 2 } / \sigma _ { 2 } ^ { 2 } } \sim F \left( n _ { 1 } - 1 , n _ { 2 } - 1 \right) \]
点估计
点估计就是用样本的某一统计量来估计总体分布中的未知参数。每个点估计都与总体参数不同,若估计量的期望值等于总体参数,则这个估计量被称为无偏估计量。使用样本均值,方差,标准差来估计总体时都是无偏的。注意,使用样本方差估计整体方差时,自由度为\(n-1\)。
区间估计
即使是无偏的点估计,在一次估计中,都与总体参数(真值)有偏差。所谓“无偏”,是指在大量重复抽样基础上的均值,是无偏的。因此,需要估计点估计与总体真实参数的偏差,即这个估计值离真实的值有多远。区间估计能根据估计量的分布,给出真实总体参数的可能范围。
若总体分布含有一个未知参数\(\beta\),找出了两个依赖于样本的估计量\(\beta_1 < \beta_2\),使得
\[ \mathrm { P } \left( \beta _ { 1 } < \beta < \beta _ { 2 } \right) = 1 - \alpha \]
其中\(\alpha \in (0,1)\),则称区间\((\beta_1, \beta_2)\)为\(\beta\)的\(100(1-\alpha)\%\)的置信区间。\(100(1-\alpha)\%\)为置信水平。有:
\[ \begin{array} { l } - Z _ { a / 2 } < \frac { \bar { X } - \mu } { \frac { \delta } { \sqrt { n } } } < Z _ { a / 2 } \\ \bar { X } - Z _ { a / 2 } \frac { \delta } { \sqrt { n } } < \mu < \bar { X } - Z _ { a / 2 } \frac { \delta } { \sqrt { n } } \end{array} \]
\[ \begin{array} { l } - t _ { a / 2 } < \frac { \bar { X } - \mu } { \frac { S } { \sqrt { n } } } < t _ { a / 2 } \\ \bar { X } - t _ { a / 2 } \frac { S } { \sqrt { n } } < \mu < \bar { X } - t _ { a / 2 } \frac { S } { \sqrt { n } } \end{array} \]
