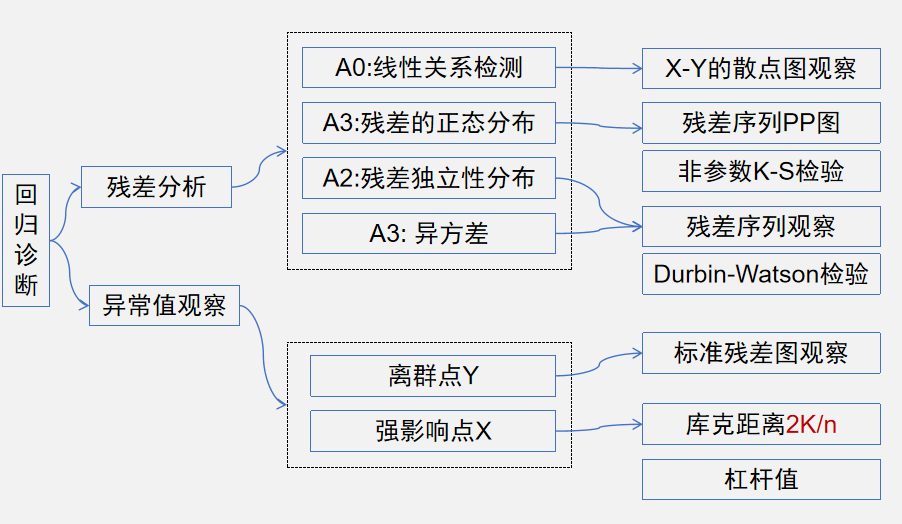
残差分析
在多元回归的章节,我们提到进行多元线性回归需要满足几个前提假定。除了假定A0,假定A1、A2以及A3都与模型拟合的残差有关。为了检验回归的结果是否满足回归分析的几个前提假定,对回归的残差进行诊断是十分有必要的。
回归诊断包括假设的检验和异常值观察案例检验两部分,假设检验通常与残差有关,因此被称为 残差检验。对于残差的检验主要包括三个方面:
- 残差是否等方差(A2:误差项齐次)
- 残差序列是否独立(A2:误差项相互独立)
- 残差是否服从正态分布(A3:正态分布假定)
残差简介
残差是指由回归方程计算所得的预测值与样本值之间的差距,即
\[ \boldsymbol { e } _ { i } = \boldsymbol { y } _ { \boldsymbol { i } } - \widehat { \boldsymbol { y } } _ { \boldsymbol { i } } = \boldsymbol { y } _ { i } - \left( \widehat { \boldsymbol { a } } + \widehat { \boldsymbol { b } } \boldsymbol { x } _ { \boldsymbol { i } } \right) \]
如果回归方程能够较好的反映被解释变量的特征和变化率,则残差中不应该包含明显的规律性和趋势性。
残差均值为0的正态性分析(A3)
当解释变量x取某个特定的值时,对应残差必然有正有负,但总体上应服从以0为均值的正态分布。正态性分析可通过绘制标准化残差的累计概率图P-P图或正态检验进行检验。
残差的独立性分析(A2)
残差序列的独立性是回归模型要求的。残差序列与残差序列的前期和后期数值之间不应存在相关关系,即不存在自相关。自相关导致模型的预测偏差较大。
残差序列的独立性分析主要有两种手段。其一是绘制残差图。
残差图Residual plot是一种散点图。若残差的均值为0,残差图中的点应在纵坐标为0的中心的带状区域内随机散落。
将样本期或者时间等作为横坐标,以残差为纵坐标,通过观察残差随着样本期或者时间的变化趋势就能大致判断残差是否存在自相关性。
第二种手段是使用Durbin-Watson检验。 DW检验推断小样本序列是否存在自相关的统计检验方法。统计量为DW。DW取值在0~4之间。DW = 0时, 完全正自相关;DW =(0,2) ,残差序列存在正自相关;DW = 2 时,残差序列独立,没有自相关;DW =(2,4) ,残差序列存在负自相关;DW = 4 时,完全负相关。
异方差分析(A2)
线性回归的另一重要假设是误差项方差齐次。若方差随着自变量或因变量取值的变化而变化,则出现异方差现象。判断残差是否出现了异方差现象也有两种手段。
出现异方差将导致最小二乘估计不再是最小方差的无偏估计,回归系数显著性检验的t值偏高,进而容易拒绝H0假设,使不该留在方程中的变量保留下来,并最终使模型的预测偏差较大。因此,有必要进行异方差分析。
其一是绘制残差的散点图。通过绘制残差与某自变量\(x_i\)的残差图,就能够判断残差是否随着自变量的增大出现更为分散/集中的趋势。
其二是等级相关分析(Spearman相关分析)。得到残差序列后对其取绝对值,然后分别计算出残差和某自变量的秩,计算Spearman等级相关系数,进行等级相关分析。拒绝等级相关分析的H0假设则认为解释变量与残差之间存在相关关系,出现了异方差。
残差分析的一般步骤为
- X和Y的线性关系分析(A0假设)
- 残差序列是否服从正态分布(A3假设)
- 残差序列是否存在异方差现象(A2假设)
- 观测间是否相互独立(A2假设)
SPSS中进行残差分析
保存回归分析的相关值
在SPSS中进行回归分析之后,可以将回归分析产生的结果(如预测值,残差等)作为一个新变量保存到数据中。使用这个保存功能能够帮助我们方便的绘图。
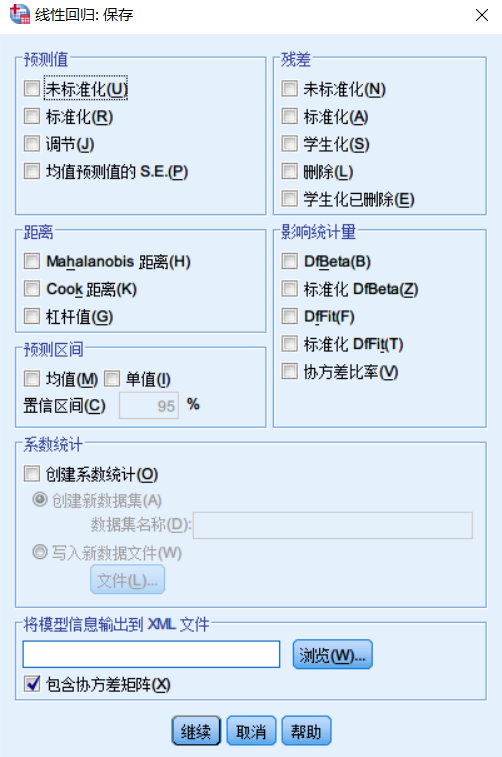
在预测值一栏,可以选择保存未标准化的预测值(根据回归模型计算的因变量的原始预测值);标准化预测值(标准化了的预测值,均值为0,标准差为1);调节后的预测值(从当前数据库中剔除当前记录拟合模型,利用模型得到的当前因变量的预测值);均值预测的S.E.(预测值的标准误,用于计算因变量预测值的可信度区间)。
在残差一栏,可以选择保存原始残差,标准化残差,学生化残差,剔除残差以及学生化剔除残差。
回归分析产生的相关值进行绘图
对于回归分析产生的相关结果(如预测值,残差等),SPSS提供了简便的绘图功能。
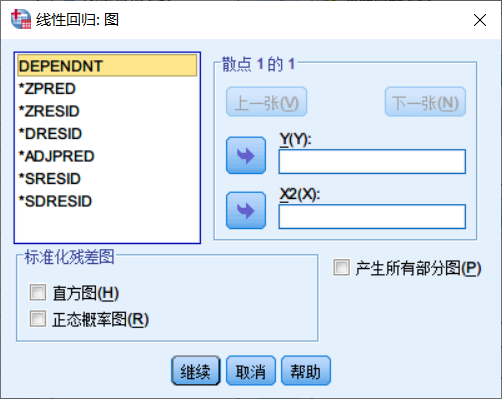
在绘图选项卡中,可以将左侧列出的变量添加到右侧的框中构造x,y轴变量绘制散点图,也可以通过勾选下方的直方图以及正态概率图分别绘制标准化残差的直方图以及P-P图。
左侧列出的变量分别为:
Dependent:因变量 ZPRED: 标准化预测值 ZRESID:标准化残差 DRESID:剔除残差 ADJPRED:修正后预测值 SRESID:学生化标准残差 SDRESID:学生化剔除残差
SPSS中具体流程
- X和Y的线性关系分析
使用图形-图表构建程序画出散点图并标上拟合线,额可以大致看出是否具有线性趋势
也可以结合使用分析-相关-双变量中的Pearson相关分析一起判断。
- 残差序列是否服从正态分布
将拟合模型的残差保存为独立变量之后,使用分析-非参数-旧对话框-1样本K-S检验残差是否符合正态分布。如果检测对应的Sig值大于0.05,则说明残差序列与正态分布不存在显著差异,残差满足了线性模型的前提要求。
- 残差序列是否存在异方差现象
首先画出残差图。根据横轴的不同,残差图的绘制也有不同的途径。绘制标准化预测值-标准化残差的残差图时,可以使用分析-回归-线性中的绘制选项卡操作;绘制自变量-标准化残差的残差图时,需要先将标准化残差保存为新变量,再使用图形-图表构建程序画出散点图。
绘制残差图后,如果发现明显存在异方差现象,则需要求残差绝对值,并使用Spearman相关分析进一步检验残差绝对值与预测值之间的等级相关性。求残差绝对值可以使用转换-计算变量进行,具体如图。
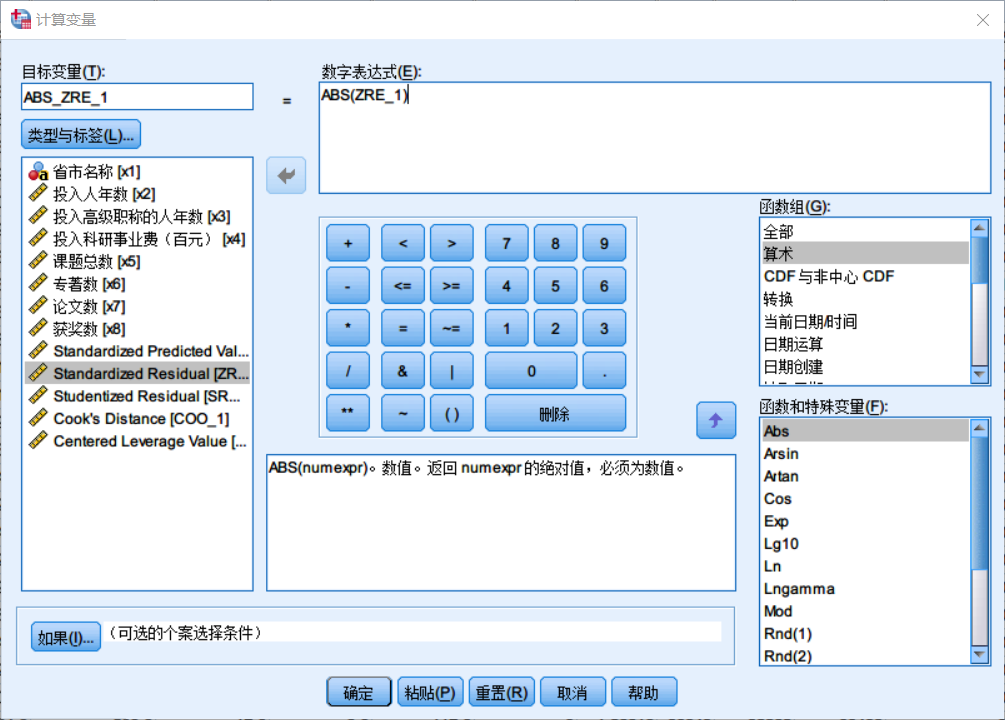
Spearman等级相关分析可以使用分析-相关-双变量来做。如果显著性检验的Sig值小于0.05,则可以认为存在异方差现象。
- 观测间是否相互独立
可以通过绘制时间变量与残差的残差图(方法同上)或者使用Durbin-Watson检验进行。DW检验在分析-回归-线性中统计量选框中可以勾选。
异常值检测
在具体的数据处理中,我们通常会发现某些观测案例在自变量或者因变量上的取值明显不同于其他大多数观测案例。这种取值有两种不同的情形:异常值(outliers)以及高杠杆率点(leverage points )。无论是哪一种都会导致回归模型对绝大多数观测案例拟合欠佳。
离群点及其检测
离群点指\(y_i\)远离模型预测值的点。产生离群点的原因很多,例如数据在收集过程中的错误记录。
离群点可以通过绘制标准化残差/学生化残差-预测值的残差图来找出。一般来说,标准化残差/学生化残差的绝对值大于3对应的观察值\(y_i\)为离群点。
在生成的残差图上双击,可以进入编辑模式。在上方的工具栏中,可以选择向Y轴添加参考线来画出+3/-3的参考线。对于在参考线以外的点,我们可以在上方的选项中选择元素-数据标签模式来单独列出这些离群值对应的数据编号。
通常来说,直接离群值删除对拟合直线的斜率和截距几乎没有影响。是否要删除需要结合杠杆率判断。
高杠杆点检测
高杠杆表示观测点\(x_i\)是异常的。单维的观测变量容易检测高杠杆点;多元情况下较复杂,单独看一个维度是在范围内的,但多维度一起观察则是高杠杆点。为了量化观测的杠杆作用,可以计算杠杆统计量(leverage statistic)。
杠杆值较高意味着对应的观察点的\(x_i\)远离其均值,它会强烈影响回归方程的拟合,是一个高杠杆点。一般情况下,若\(h_i\)大于2-3倍的h均值,则可认为其观察值为高杠杆点。
库克距离:按照经验,库克距离大于2K/n(K为估计系数的个数包括截距项,n为样本量)通常认为对应的观察值为高杠杆点。
使用散点图进行异常值检测
可以使用散点图对高杠杆点以及离群点进行统一检测。在分析-回归-线性中保存选框中,我们可以勾选标准化以及Cook距离两项进行保存。然后,我们可以借助保存的变量,以cook距离为x轴,标准化残差为y轴画出散点图。最后,我们根据模型以及样本数计算2K/n,通过分别在下x,y轴上绘制参考线的方式找出高杠杆点以及离群点。通常来说,如果一个样本既是高杠杆点也是离群点,我们会考虑删去它再进行一次回归分析。绘图例子如下。
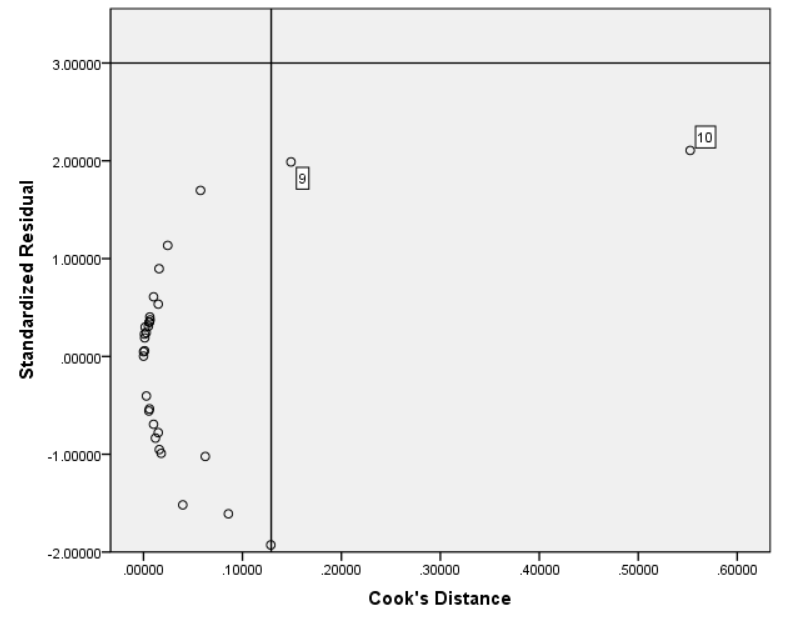
总结如下。