多因素方差分析基本思想
多因素方差分析用来研究两个及两个以上控制变量对观测变量产生显著影响。其不仅可以分析多个因素对观测变量的独立影响,更能够分析多个控制因素的交互作用能否对观测变量的分布产生显著影响。
多因素方差分析通过变异分解将样本的总变异分解为若干部分,除一部分代表随机误差的作用外,其余每个部分的变异分别代表某个影响因素的作用。通过比较可能由某因素所致的变异与随机误差的大小,借助F分布做推断,即可了解该因素对结果变量的影响是否存在。
多因素方差分析(以双因素为例)
观测变量的变动受以下三个方面的影响:控制变量独立作用;控制变量交互作用以及随机因素。观测变量的总变差可分解为(在双因素\(A,B\)的情况下):
\[ SST = SSA+SSB+SSAB+SSE \]
其中\(SSA+SSB\)被称为主效应,\(SSAB\)被称为交互效应,\(SSE\)被称为残差。
直观理解交互作用

假设分别有性别\(F,M\)以及职位(蓝领,白领)分别影响收入,在上图所示的情况中不存在两个因素之间的交互作用。因为有:1. 无论是\(F,M\),都有白领收入高于蓝领;2. 无论是蓝领还是白领,都有\(M\)的收入高于\(F\)。
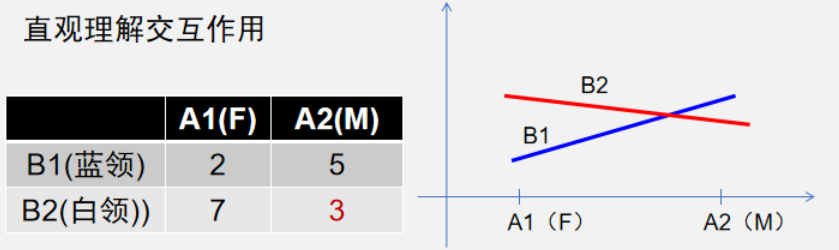
在上述情况中,如果是\(F\)则有白领收入高于蓝领,如果是\(M\)则有蓝领收入高于白领。所以性别和工作性质是有关的。收入情况同性别和工作性质的组合有关联。这说明两个因素之间存在着交互作用。
如果一个因素的效应大小在另一因素不同水平下明显不同,则称为两因素间存在交互作用。当发生了交互作用时,单纯研究某个因素的作用是没有意义的。必须分另一个因素的不同水平研究该因素的作用大小。
固定效应与随机效应
在多因素方差分析中,控制变量可以进一步分为固定效应(给观测变量带来的影响是固定的)和随机效应(制变量的各个水平无法做严格的控制,它们给观测变量带来的影响是随机的)两种类型。一般区分固定效应和随机效应比较困难。由于这两种效应的存在,多因素方差分析模型也有固定效应和随机效应模型之分,差别体现在检验统计量的构造上。
一般而言,固定因素和随机因素在分析的时候应该分别指出,如果将随机因素按固定因素来分析,则可能得出错误的分析结果。有时候区分固定因素和随机因素并不容易。把握以下原则:区分二者并不是该因素本身的特性,而是分析的目的。如果将其看做固定因素,研究结论就不应当外推到未出现的其他水平中去;否则应将其考虑为随机因素来分析。
固定效应模型的统计量
分析步骤为:
- 确定观测变量和若干个控制变量
- 剖析观测变量的方差
- 分别比较观测变量总离差平方和各部分所占的比例,推断控制变量以及控制变量的交互作用是否给观测变量带来了显著影响。
固定效应模型中,先对A,B的效应进行判断,再对AB的交互作用进行检验。具体统计量为:
\[ \begin{aligned} & F_A = \frac{SSA/(k-1)}{SSE/kr(l-1)}\\ & F_B = \frac{SSA/(r-1)}{SSE/kr(l-1)}\\ & F_{AB} = \frac{SSAB/(k-1)(r-1)}{SSE/kr(l-1)} \end{aligned} \]
其中\(k\)为控制变量\(A\)的水平数,\(r\)为控制变量\(B\)的水平数,\(l\)为每个交叉水平下的样本数。
统计量的原假设为各控制变量不同水平下观测变量各总体的均值无显著差异。
随机效应模型的统计量
分析步骤和原假设与固定效应相同。不同之处除了统计量构造外,在随机效应模式中,首先对A,B的交互作用是否显著进行推断,然后再分别依次对A,B的效应进行检验。统计量分别为:
\[ \begin{aligned} & F_A = \frac{SSA/(k-1)}{SSAB/(k-1)(r-1)}\\ & F_B = \frac{SSA/(r-1)}{SSAB/(k-1)(r-1)}\\ & F_{AB} = \frac{SSAB/(k-1)(r-1)}{SSE/kr(l-r)} \end{aligned} \]
SPSS中的多因素方差分析
使用分析-一般线性模型-单变量可以进行多因素方差分析。分析结果如下图:
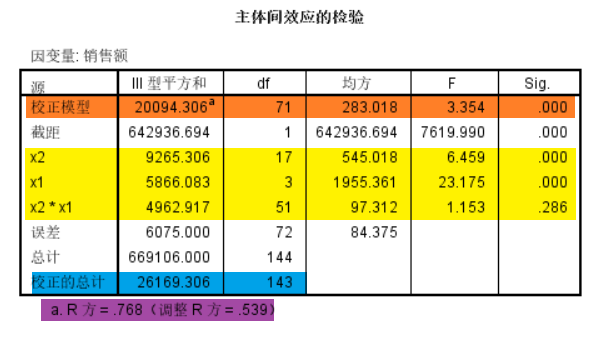
图中有控制变量x1,x2,观测变量的总变差为26169.06,总变差可以被分成四个部分,由x1解释的变差(5866.083),由x2解释的变差(9265.308),由两部分相互作用解释的变差(4962.917)以及随机因素造成的误差(6075.000)。其中三个F统计量(黄色部分)对应的Sig值分别为0.00,0.00,0.286。这说明x1,x2单独都对观测变量有显著的影响,但两者的交互作用未对观测变量差生显著作用。
另外,橙色部分的校正模型解释的总变差是x1,x2,x1*x2相加的结果,是线性模型整体对观测变差解释的部分,其对应的F统计量3.354和概率值0.00,说明观测变量变动主要是某控制变量总体的不同水平引起的,控制变量能够较好地反映观测变量的变动,模型对观测变量有一定的解释能力。
紫色部分的R方以及调整后的R方反映的是多因素方差模型对观测变量数据的总体拟合程度。越接近1,表明对数据拟合程度越高。本问题中调整后的R方为0.539,说明除了x1,x2之外,观测变量还受其他因素的影响。
非饱和模型
双因素方差分析的总变差可以分解为:
\[ SST = SSA+SSB+SSAB+SSE \]
如果进一步研究发现,控制变量的某阶交互作用没有给观测变量产生显著影响,则可以尝试建立非饱和模型。
\[ SST = SSA+SSB+SSE \]
SPSS中建立非饱和模型,可以点击模型按钮,在弹出框中的指定模型中选择设定,并通过调整构建项中类型来将左边的因子添加到右边的模型中。
均值比较
- 多重比较检验
如果通过多因素方差分析得知某控制变量的不同水平对观测变量产生显著影响,进一步可对各水平间的均值进行精细比较。同单因素方差分析,根据方差齐次性检验,选择合适的多重比较检验方法。 在SPSS中,同样是通过两两比较选项进行多重比较方法的选择。
- 边界均值和轮廓图(交互作用图形分析)
基于现有模型,当控制了其他因素的作用后,依据样本情况计算出的用于比较的各水平的均值估计值。可用轮廓图呈现。轮廓图可以用于比较各种水平组合下均值的变化规律,寻找可能存在的交互作用非常有用。相互平行意味着不存在交互作用,大量的交叉说明交互作用的存在。
在SPSS中,可以通过绘制选项中将两个变量分别添加到水平轴和单图框中,点击添加按钮绘制。绘制结果如下图:
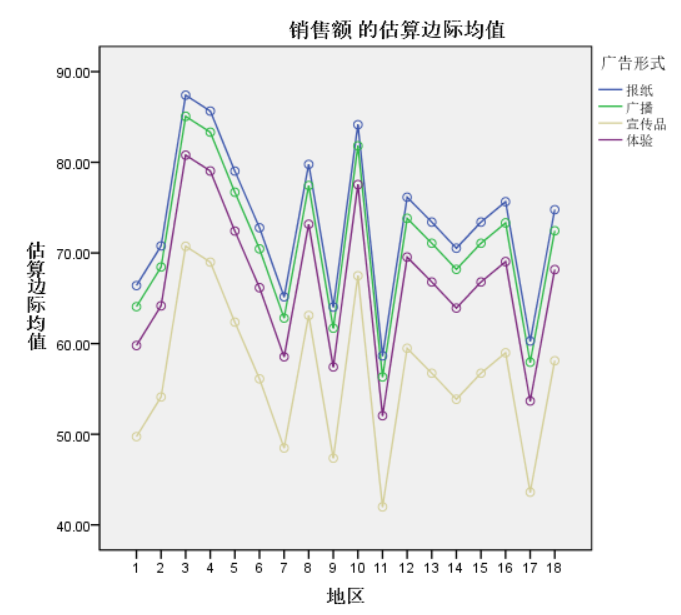
用例子来说明的话,如上图中的黄色线就是在广告形式为宣传品的前提下,各个地区销售额的均值走势。由于上述折线基本平行,直观结论是两个因素间不存在交互作用。
事后检验
当交互效果显著时,主效果是一个过度简化,没有考虑到其他因子的检验。如果直接对某一显著的主要效果加以解释或讨论,会扭曲该因子的真实效果;故需进行进一步的事后检验程序:包括单纯主效果,如果显著,还应进行多重比较。
说人话就是,因为交互效应显著,所以单纯使用单因素或者多因素方差分析的话很难确定单个控制变量独自对观测变量存在多大的影响(因为存在与其他因子的交互作用)。
为了确定单个控制变量独自对观测变量存在多大的影响,需要控制与其存在交互效应的另一个变量,对另一个变量在不同取值下的样本进行分情况讨论。
举个例子,假如两个控制变量A,B交互效应显著,现在想要探讨变量A独自对观测变量存在多大的影响,就应该根据变量B的各个水平拆分数据集,在每个拆分后的数据集上对变量A进行单因素方差分析,如果显著的话可以进行事后多重比较。最后通过分情况讨论得出结果。
