多元线性回归的基本概念
回归分析利用线性关系来进行解释与预测。通常在一个研究中,影响因变量的解释变量不止一个,则需要建立包含多个解释变量的多元回归模型。
多元回归模型的假定条件
与简单回归一样,多元回归方程进行参数估计时仍然采用常规最小二乘法。在多元回归模型中,采用这种方法需要以下几个基本假定。
- A0模型设定假定(线性假定) 自变量与因变量之间存在线性关系;可通过散点图矩阵予以考察;若非线性关系,可以通过变量变换予以修正
- A1正交假定 假定误差项矩阵\(\varepsilon\)与\(X\)中的每一个向量\(x\)都不相关。即\(\operatorname{Cov}(X, \varepsilon) = 0\)。该假定保证了我们对回归模型参数的最小二乘估计是无偏的。
A2独立同分布假定 该假定是针对总体回归模型的误差项,要求他们满足彼此之间相互独立,并服从同一分布的条件。具体来说,
- 独立分布:每一个误差项\(\varepsilon_i\)为独立分布,即\(\operatorname{Cov}(\varepsilon_i, \varepsilon_j)=0, i\neq j\)。
- 同方差性:即满足\(\operatorname{Var}(\varepsilon_i)= \sigma_i^2 = \sigma^2, i=1,2,...,n\)。
A3正态分布假定 在A2假定的基础上,这个假定进一步要求\(\varepsilon_i\)服从正态分布\(N(0,\sigma^2)\)。正态分布使得最小二乘法估计可以被理解为最大似然估计。但是正态分布假定主要应用于对回归参数的估计值进行统计检验的情况,且只有在小样本情况下才需要注意这个问题。对于大样本来说,根据中心极限定理,即使误差项不满足正态分布,我们仍然可以对回归参数的估计值进行统计推断。
多元线性回归的基本流程
多元回归与一元回归相同,在进行分析之后,都需要进行拟合优度检验,回归方程整体显著性检查以及回归系数显著性检查。但是与一元回归不同的是,多元回归还需要考虑多重共线性问题,并需要进行残差分析。
使用SPSS中的分析-回归-线性可以进行多元回归。对于回归结果的拟合优度检验,回归方程整体显著性检查以及回归系数显著性检查在一元回归中已经阐述果,在此不再进行详述。
在多元回归分析中,由于被解释变量会受众多因素的共同影响,需要由多个解释变量解释,于是会出现如下问题:多个变量是否都能够进入模型;解释变量应以怎样的策略和顺序进入方程;方程中多个解释变量之间是否存在多重共线性等问题。解决这三个问题要从多重共线性问题入手。
多重共线性问题
共线性问题是影响多元回归分析最重要的因素之一。多重共线性指解释变量之间存在线性相关的现象。解释变量间高度的多重共线性会给回归方程带来影响。比如会出现偏回归系数估计困难(完全多重共线性的情况);偏回归系数的估计方差随解释变量相关性的增大而增大;偏回归系数估计值不稳定性增强等等不良后果。
判断是否出现多重共线性问题可以有两个角度,分别是从模型表现来看以及从模型指标来看。就模型表现来说,出现以下几种情况,可以猜测多元回归模型中存在这多重共线性问题:
- 整个模型检验结果有效\(p<\alpha\),自变量偏回归系数的统计检验结果\(p > \alpha\)
- 专业上认为有统计需意义的自变量检验结果无统计学意义
- 偏回归系数取值大小甚至符号与实际情况相悖,难解释
同时,也有许多指标可以反映模型多重共线性问题的严重程度。
容忍度
当自变量\(X_i\)与其他所有自变量\(X_t, X_s...\)的复相关系数\(R_i\)接近1,则自变量具有明显的多重共线性。此时定义容忍度指标\(\operatorname{Toli} = 1 - R_i^2\)。容忍度越小,共线性越强。
复相关系数是测量一个变量与其他多个变量之间线性相关程度的指标。它不能直接测算,只能采取一定的方法进行间接测算。通常,测量\(y\)与一组变量\(x_1, x_2...,x_k\)之间的相关系数,可以使用线性回归构造一个关于\(x_1, x_2...,x_k\)的线性组合,通过计算该线性组合与\(y\)之间的简单相关系数来作为变量\(y\)与\(x_1, x_2...,x_k\)之间的复相关系数。
方差膨胀因子
方差膨胀因子\(\operatorname{VIF}= 1/ \operatorname{Toli}\)。VIF大于等于1。解释变量间的多重共线性越弱, VIF越接近1。反之,共线性越强,VIF越大。当自变量中最大的VIF大于10,且平均VIF显著大于1,则说明存在严重的共线性问题。
特征根
从解释变量(自变量)的相关系数矩阵出发,计算相关系数矩阵的特征根(主成分)。特征根越小,表示解释变量间具有共线性,当特征根为0时,表示解释变量间有完全的线性相关性。
条件指数
最大特征根与当前特征根的比值的算术平方根。反应多重共线性的指标。
\[ K_i = \sqrt{\frac{\lambda_m}{\lambda_i}} \]
第\(i\)个条件指数\(K_i\)为最大特征根\(\lambda_m\)与第\(i\)个特征根比值的平方根。显然如果\(K_i\)越大,则说明解释变量间的信息重叠较多,多重共线性较为严重。一般情况下认为>100很严重,10-100之间则认为多重共线性强。
方差比
是指模型中各自变量(包括常数项)的变异被各特征根解释的比例,或者各特征根对模型中各变量的贡献。如果某特征根对两个或多个变量贡献均较大(>0.5),说明这几个变量间存在一定程度的共线性。
使用SPSS中的分析-回归-线性,并在统计量选项框内勾选共线性诊断,则可以输出共线性分析报告。
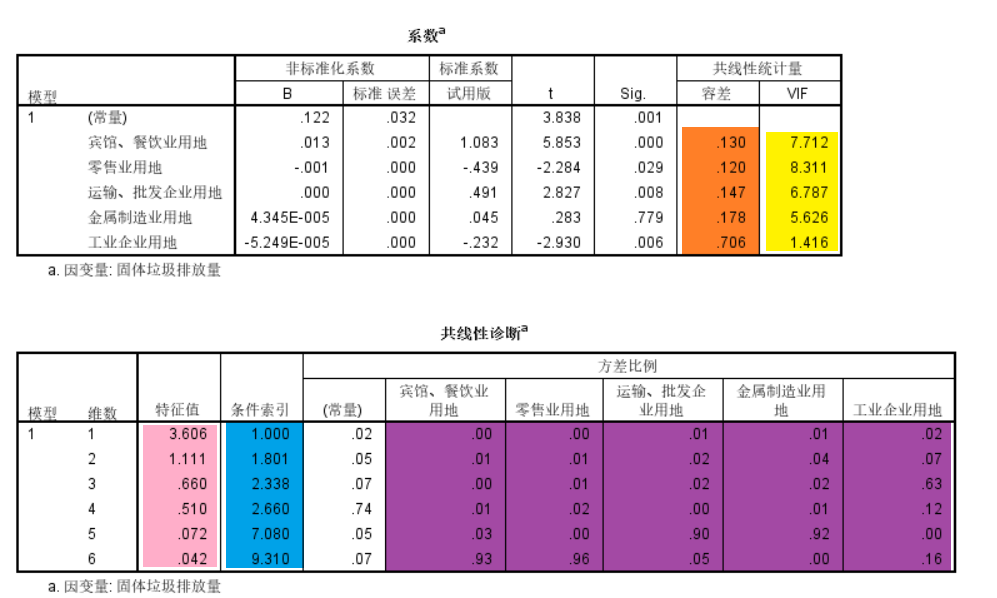
报告中,容忍度(橙色)与方差膨胀因子(黄色)在一个表中,而特征根(粉色)、条件指数(蓝色)与方差比例(紫色)在一个表格内。
在本例子中,特征根6对应宾馆,餐饮业用地以及零售业用地都有较高的方差比例,同时特征根5对应运输、批发企业用地以及金属制造业用地也有较高的方差比例,这说明这两对变量内部可能存在着一定的多重共线性问题。(一般在研究的时候不会将常量对应的方差比例纳入考虑)。
