因子分析简介
在研究实际问题的过程中需要尽可能收集相关变量,旨对问题有全面完整的把握与认识。但在实际建模时,变量多未必能真正发挥预期作用,反而会给统计分析带来许多问题,主要表现在计算量问题以及变量相关性问题上(变量信息间的高度重叠和相关会给统计方法的应用带来障碍。如多元回归中的“多重共线性的问题”)。
虽然变量间相关性的问题可以通过削减变量个数来解决,但是变量个数的削减也会导致信息的丢失与不完整。因此,我们需要一个方法,既能够大大减少参与数据建模的变量个数,也不会造成信息的大量丢失。
因此,我们可以使用因子分析。因子分析以最少的信息丢失为前提,将众多的原始变量综合成较少的综合指标,名为因子factor。因子分析中的因子具有以下特点:
- 因子个数远小于原有变量个数
- 因子能够反应原有变量的绝大部分信息
- 因子间的线性关系不显著
- 因子具有命名解释性
因子分析的数学模型
因子分析的核心是用较少的互相独立的因子反映原有变量的绝大部分信息。变量\(X_i(i=1 \cdots p)\)用\(m\)个因子\(F_i(i=1 \cdots m)\)的线性组合来表示。其中对于变量\(X_i\),可以表示为:
\[ X _ { i } = a _ { i 1 } F _ { 1 } + a _ { i 2 } F _ { 2 } + \cdots + a _ { i m } F _ { m } + \varepsilon _ { i } \]
所有的变量用因子反映的线性组合可以用矩阵来表示:
\[ \left[ \begin{array} { c } X _ { 1 } \\ X _ { 2 } \\ \vdots \\ X _ { p } \end{array} \right] = \left[ \begin{array} { c c c c } a _ { 11 } & a _ { 12 } & \cdots & a _ { 1 m } \\ a _ { 21 } & a _ { 22 } & \cdots & a _ { 2 m } \\ \vdots & \vdots & & \vdots \\ a _ { p 1 } & a _ { p 2 } & \cdots & a _ { p m } \end{array} \right] \left[ \begin{array} { c } F _ { 1 } \\ F _ { 2 } \\ \vdots \\ F _ { m } \end{array} \right] + \left[ \begin{array} { c } \varepsilon _ { 1 } \\ \varepsilon _ { 2 } \\ \vdots \\ \varepsilon _ { p } \end{array} \right] \]
我们称\(F_i(i=1 \cdots m)\)为公共因子,是不可观测的变量,他们的系数称为因子载荷。\(\varepsilon_i(i=1 \cdots p)\)是特殊因子,是变量中不能被前\(m\)个公共因子包含的部分。其中有:
- \(\operatorname{cov}(F,\varepsilon)=0\),即公共因子与特殊因子之间相互独立。
- 公共因子互相之间相互独立。
在因子不相关的前提下,因子载荷\(a_{ij}\)是变量\(X_i\)与因子\(F_j\)的相关系数。反映的是\(X_i\)与\(F_j\)的相关程度。同时也反映了因子\(F_j\)对解释变量\(X_i\)的重要作用和程度。
因子分析的相关概念
我们使用一个例子来进行说明。若要根据学生的代数1,2,几何,三角以及解析几何的分数使用因子分析评定学生的能力,可以建立下述因子分析模型:
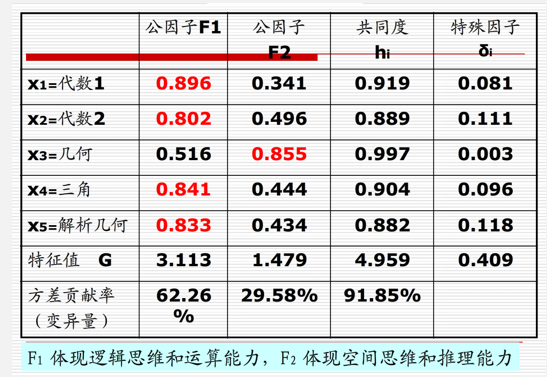
- 共同度
又称共性方差或公因子方差,就是变量与每个公共因子的负荷量的平方总和。记为:
\[ h _ { i } ^ { 2 } = \sum _ { j = 1 } ^ { m } a _ { i j } ^ { 2 } \]
从共同度的大小可以判断原始变量与当前因子分析模型之间的关系程度,同时刻画了因子全体对变量\(X_i\)信息解释的程度,是评价变量\(X_i\)信息丢失程度的重要指标,衡量因子分析效果的重要依据。如当前案例中,有:
\[ h_1^2=(0.896)^2+(0.341)^2 = 0.919 \]
- 特征值
是第\(j\)个公共因子\(F_j\)对于每一个自变量\(X_i\)提供的方差的总和,又称为第\(j\)个公共因子的方差贡献。再本案例中有\(F_1\)的特征值\(G\):
\[ G=(0.896)^2+(0.802)^2+(0.516)^2+(0.841)^2+(0.833)^2=3.113 \]
- 方差贡献率
指公共因子对实测变量的贡献,又称为变异量。方差贡献率=特征值\(G\)/实测变量数\(p\)。
它是衡量公共因子相对重要性的指标,方差贡献率越大,表明公共因子对自变量的贡献更大,重要性更高。本案例中因子\(F_i\)的方差贡献率为:
\[ 3.113/5 = 62.56\% \]
因子分析的基本步骤
因子分析的基本步骤如下:
- 前提条件签定
考察原始变量之间是否存在较强的相关关系。如果原有变量相互独立,不存在信息重叠,就不需要因子分析。
- 因子提取
在样本数据的基础上提取因子
- 因子旋转
通过正交旋转或者斜交旋转使提取出的因子具有可解释性
- 因子得分
通过各种方法求解个样本在各个因子上的得分,为进一步分析奠定基础
前提条件签定
主要有三个方法:
- 相关系数矩阵;如果矩阵中大部分相关系数值都小于0.3,即各变量之间大多为弱相关,原则上这些变量不适合进行因子分析。
- 巴特利球度检验;其原假设为相关系数矩阵为单位矩阵,即原始变量之间无相关关系。若Sig小于给定的显著性水平时,说明原假设不成立,变量之间存在相关关系。
- KMO检验;KMO检验的统计量时用于比较简单相关系数矩阵和偏相关系数的指标。Kaiser给出了KMO的度量标准:0.9以上表示非常适合,0.8表示适合,0.7表示一般,0.6表示不太适合,0.5以下表示极不适合。
因子提取
通常使用主成分分析法。具体证明此处省略。在主成分分析的实际应用中,一般只选取前面特征根较大的n个主成分。n小于原始变量个数,这样就减少了变量个数(降维),又能用较少的主成分变量反映原有变量的绝大部分信息。具体步骤如下:
- 将原有变量数据进行标准化处理
- 计算变量的简单相关系数矩阵R
- 求相关系数矩阵R的特征根\(\lambda_1 \ge \lambda_2 \ge \cdots \ge \lambda_p \ge 0\)及对应的单位特征向量\(\mu_1, \mu_2, \cdots , \mu_p\)。
- 利用特征根以及特征向量计算因子载荷矩,作为因子分析的初始解。
\[ A = \left[ \begin{array} { c c c c } a _ { 11 } & a _ { 12 } & \ldots & a _ { 1 p } \\ a _ { 12 } & a _ { 22 } & \ldots & a _ { 2 p } \\ \ldots & \ldots & \ldots & \ldots \\ a _ { p 1 } & a _ { p 2 } & \ldots & a _ { p p } \end{array} \right] = \left[ \begin{array} { c c c c } \mu _ { 11 } \sqrt { \lambda _ { 1 } } & \mu _ { 21 } \sqrt { \lambda _ { 2 } } & \ldots & \mu _ { p 1 } \sqrt { \lambda _ { p } } \\ \mu _ { 12 } \sqrt { \lambda _ { 1 } } & \mu _ { 22 } \sqrt { \lambda _ { 2 } } & \ldots & \mu _ { p 2 } \sqrt { \lambda _ { p } } \\ \ldots & \ldots & \ldots & \ldots \\ \mu _ { 1 p } \sqrt { \lambda _ { 1 } } & \mu _ { 2 p } \sqrt { \lambda _ { 2 } } & \ldots & \mu _ { p p } \sqrt { \lambda _ { p } } \end{array} \right] \]
为了实现将降维,我们在计算因子载荷矩阵时,通常只选取前\(k\)个特征值以及对应的特征向量。确定因子数\(k\)主要有两种方法:
- 根据特征根\(\lambda_i\)确定因子数。观察各个特征根的值,一般选取特征根大于1的特征根;另外,还可以绘制特征根数与特征根值的碎石图(Scree plot)来确定因子数。(由陡到平缓的转折点作为分界线)
- 根据因子的累计方差贡献率确定因子数。通常选取累计方差贡献率大于0.85时的特征根个数为因子个数\(k\)。
因子旋转
经过上述步骤,我们可以得到需要的因子,但是这些因子通常因子载荷非常分散,不具有解释性。而在实际分析工作中,我们希望的是对因子的实际含义有比较清楚的认识。
使用因子旋转的方法,我们可以使一个变量在尽可能少的因子上有比较高的载荷(即使新的载荷系数尽可能接近0或者远离0)。将因子载荷矩阵A左乘一个正交矩阵r后得到一个新的矩阵B,它不影响变量\(X_i\)的共同度,只改变因子的的方差贡献。因子旋转通过改变坐标轴,能够重新分配各个因子解释原始变量方差的比例,使因子更容易被理解。
因子旋转的方法大致能分成两类:正交旋转:坐标轴在旋转的过程中始终保持垂直,因而新生成的因子仍然可保持不相关性;斜交旋转:坐标轴可以是任意角度,以牺牲因子的独立性为代价,但能够得到比较好的解释因子。
正交旋转也可以分为方差最大旋转(简化对因子的解释);四次最大正交旋转(简化对变量的解释)以及等量正交旋转三种。一般使用的是方差最大旋转。
因子得分
前面我们主要解决了用公共因子的线性组合来表示一组观测变量的有关问题。如果我们要使用这些因子做其他的研究,比如把得到的因子作为自变量来做回归分析,对样本进行分类或评价,这就需要我们对公共因子进行测度,即给出公共因子的值。
各个样本在给定因子上的得分可以通过因子载荷矩阵的权重进行计算。
在SPSS中使用因子分析(主成分回归)
本案例需要从1988年汉城奥运会男子十项全能的真实竞赛成绩出发,分析出决定男性运动员十项全能总成绩的主要运动能力,以便有针对性地更快,更好地进行运动员的选拔和培养。
分析主要是为了解决以下问题:
- 十项全能运动主要测验运动员哪几方面的运动能力?
- 上述这些运动能力在决定十项全能总分方面的重要程度?
- 根据上述运动能力培养运动员时,应当以哪些运动成绩的提高为主要测量标准?
由于十项运动反映的运动能力坑定存在重叠,因此我们需要引入因子分析进行降维。但在此之前,我们先引入所有变量建立多元线性回归模型。
使用分析-回归-线性建立简单线性模型,得出结果如下:
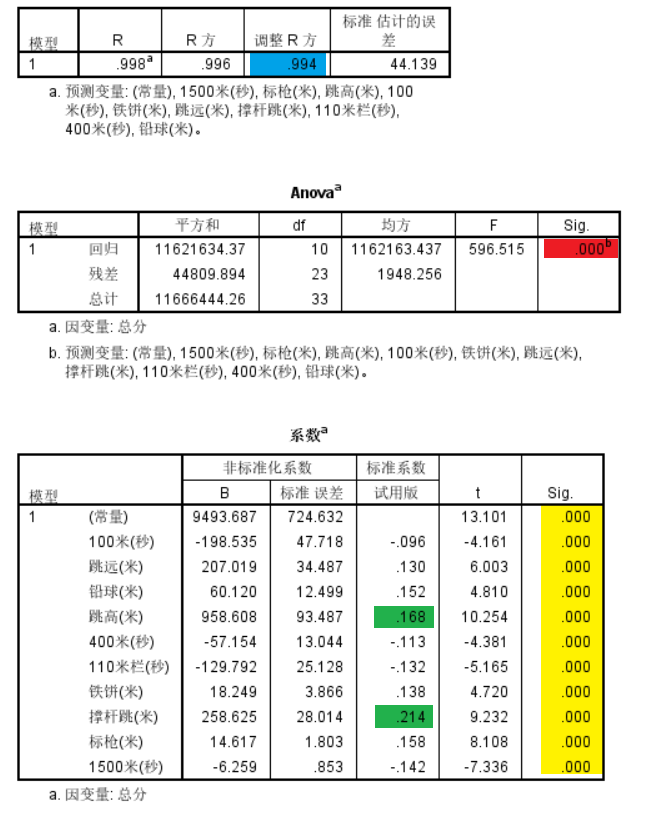
从结果中可以看出,模型的调整后R方(蓝色)为0.994,说明模型拟合效果很好。单因素方差分析的Sig值为0(红色),对应F统计量值为596.515,说明模型整体显著性很高,自变量与因变量之间关系显著。对于模型各个自变量回归系数的显著性分析Sig值都小于0.05(黄色),说明尽管自变量间存在较大的相关性,每项运动都具有统计学意义,自变量的相关性并未导致模型严重失真,回归系数大小正常,从系数上观察,跳高和撑杆跳(绿色)似乎最重要。
接下来我们使用因子分析进行检验。
前提条件签定
我们可以通过相关矩阵以及KMO-Barlett's球形检验来判断样本是否适合因子分析。我们可以使用分析-降维-因子分析进行整个流程的分析。在界面右侧点击描述,勾选系数,显著性水平,KMO和Barlett的球形检验生成分析结果。
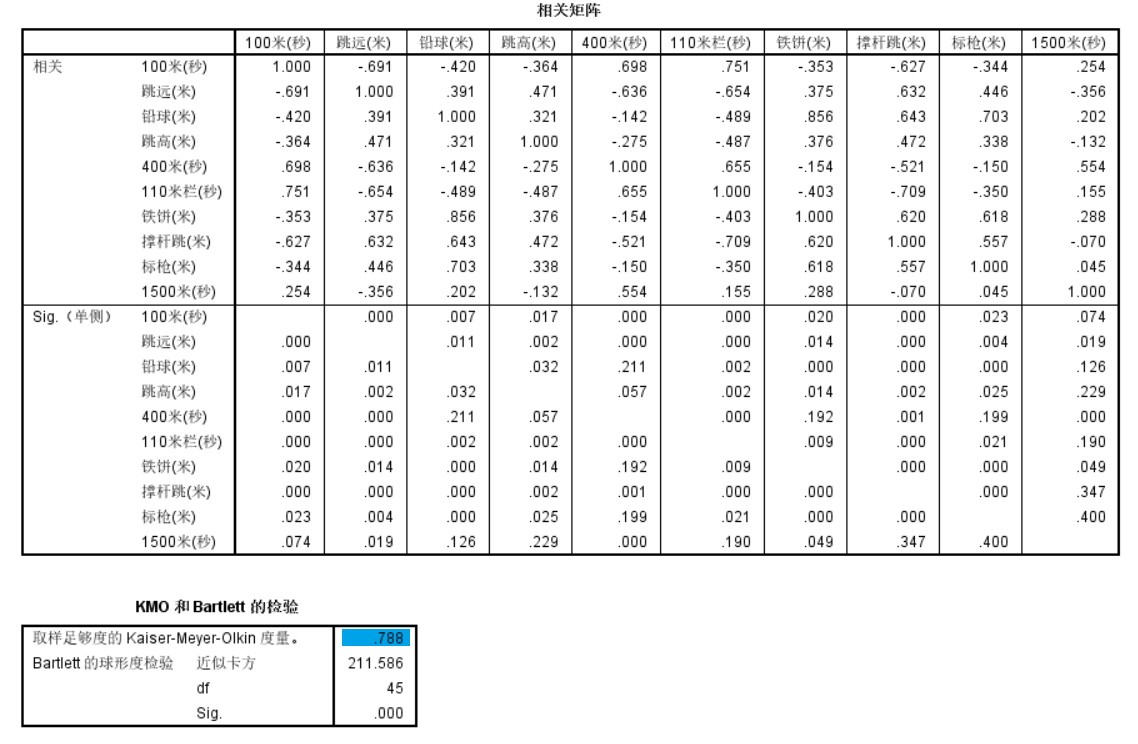
可以看到由许多变量之间的相关性在0.05的显著性水平下超过了0.3,证明变量之间存在较强的相关性。同时,样本的KMO的统计量为0.788,而且Barlett球形检验的Sig值也小于0.05,这说明变量之间存在明显相关性,可以进行因子分析。
因子提取
点击抽取按钮,选择碎石图,可以帮助选择提取因子的个数。
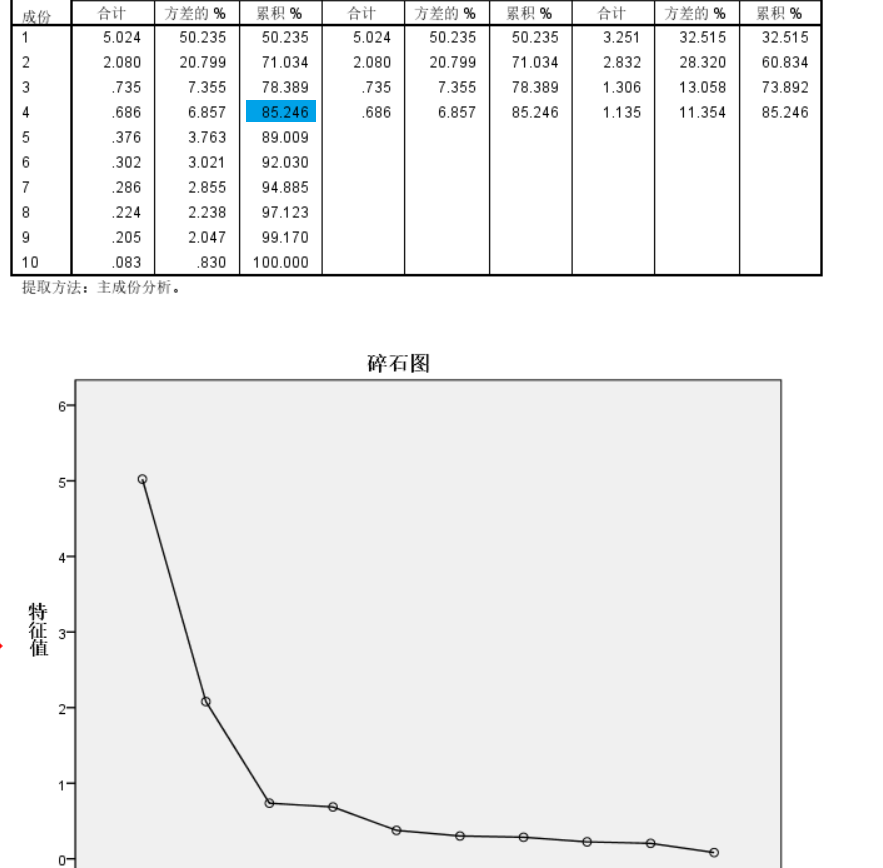
解释的总方差表显示,第1,2公因子的特征根的值远大于1,两者合计携带了71%的原始信息量,3-4公因子的特征根明显小于1,从数据浓缩的角度讲,似乎不需要提取。使用碎石图能更好反映特征根值的变化。从碎石图可以看出,第3,4因子的特征根虽然小于1,但明显高于5-10公因子,而且直到第4因子,模型解释的总方差才超过了85%。从解释数据内在关联性的角度考虑,我们将第3,4因子也加入模型。
因子旋转
提取因子后,四个因子与自变量构成的因子载荷矩阵如下图:
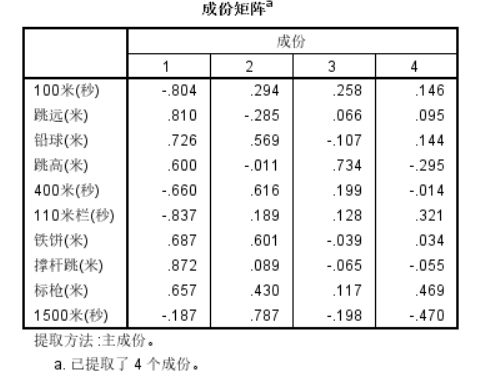
从图中可以看出,若以因子载荷等于0.5作为解释性强弱的分界线,第1因子对于除了1500米之外几乎所有的项目都具有较强的解释性,而第4因子对于所有项目都不具有较强的解释性。这显然是我们不愿看到的。因此,通过因子旋转,我们希望使一个变量在尽可能少的因子上有比较高的载荷。
在界面中选择旋转选项,选择最大方差法,勾选输出旋转解即可进行因子旋转。
旋转后的因子载荷矩阵如下图:
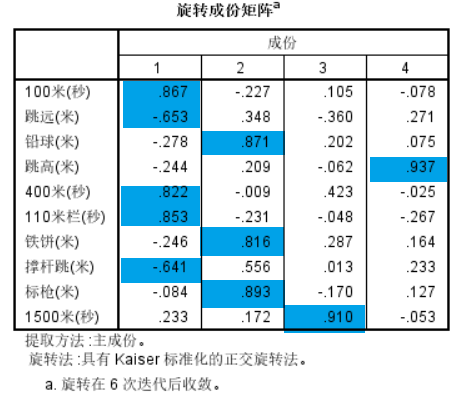
根据因子载荷的值我们可以总结,第1因子主要与短跑类运动相关,可以命名为短跑冲刺能力;第2因子主要与投掷相关,可以命名为投掷能力;第3因子主要与中长跑相关,可以命名为中长跑耐力;第4因子主要与调高相关,可以命名为弹跳力。至此,我们可以回答第一个问题。
因子得分
在界面中点击得分选项,勾选保存为变量,显示因子得分系数矩阵,并在方法栏中选择回归即可将各个自变量在提取出的因子上的得分保存到变量集中。
主成分回归
为了明确提取出的四个因子是否能解释因变量的变化,每个因子对于因变量变化的重要性如何,我们可以用提取出的4个因子代替10个原始变量进行与总分的回归预测,建立相应的回归模型。
具体步骤参照多元回归一节,在此不再赘述。结果如下:
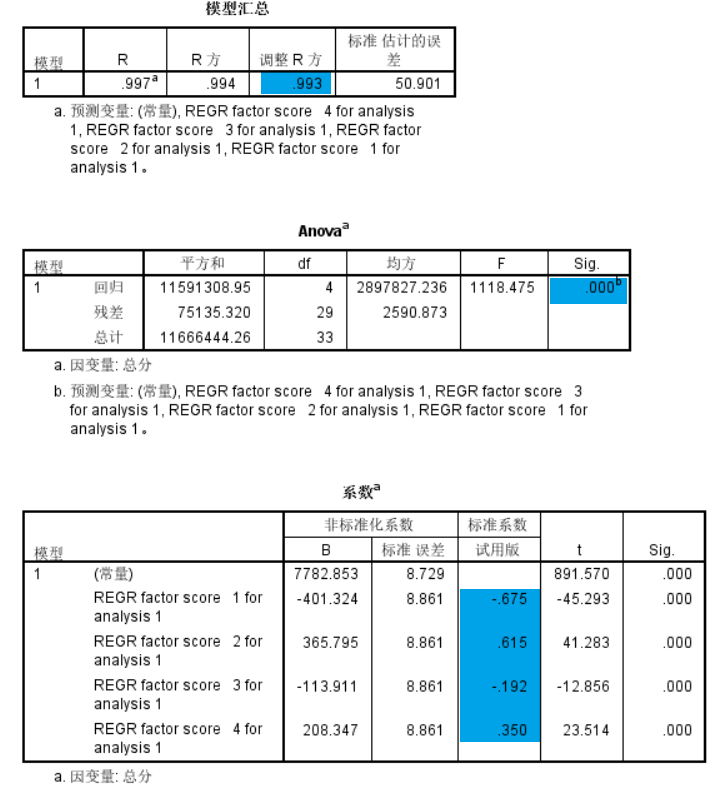
使用降维后4个因子构建的模型的调整R方为0.993,在使用了85%原始信息量的情况,调整系数只降低了0.002,说明绝大多数有效信息都在公因子中得到了保留。
由标准化的回归系数可以看出,第1,2因子,也就是长跑和投掷能力对于成绩的影响比较重要。至此,我们可以回答第二个问题。
主成分还原
为了达到第三个目标,需要了解原始自变量在回归方程中的重要性依次是多少。由于直接建模所得到的回归方程存在多重共线性,因此结果并不可靠。我们可以将主成分回归方程还原回原始变量的形式,得到更为稳妥的分析结果。
为了将主成分回归方程还原为原始变量的形式,我们可以使用旋转后的因子载荷矩阵乘上主成分回归方程的标准化回归系数。最终我们可以得到:
\[ \begin{aligned} Score =& -0.120 Z100米+0.178 Z跳远+0.1407 Z铅球\\ &+0.17 Z跳高-0.115 Z400米-0.123 Z110米栏+0.130 Z铁饼\\ &+0.159 Z撑杆跳+0.182 Z标枪-0.108 Z1500米 \end{aligned} \]
方程中的标准化系数和原始变量直接进行回归所得到的系数有明显的差异,从现有方程得知,标枪,跳远和跳高是对总分影响最大的3个项目,而不是原回归模型中的撑杆跳项目。至此,我们可以回答最后一个问题。
