方差分析概述
方差分析从观测变量的方差入手,研究控制变量(自变量)的差异对观测变量(因变量)是否存在显著影响。其中控制因素通常为分类变量,而观测变量通常为连续变量。导致观测变量值变化的因素通常有两类:控制因素(自变量)不同水平的影响;随机因素的影响,主要指试验过程中的抽样误差。方差分析认为,如果控制变量的不同水平对观测变量产生了显著影响,那么它和随机变量共同作用必然使得观测变量值发生显著变动。反之,如果观测变量值在控制变量的各个水平中没有出现明显波动,则认为该控制变量没有对观测变量产生作用(即自变量和因变量之间不存在关联),数据波动是抽样误差造成的。
方差分析通过推断控制变量各水平下观测变量的总体分布是否有显著差异来实现分析的目的。而总体分布的差异的判断主要是通过总体均值显著性检验来实现的。
方差分析对观测变量各总体的分布有以下两个基本假设:观测变量各总体服从正态分布; 观测变量各总体的方差应相同。根据控制变量的个数,方差分析分为单因素方差分析,多因素方差分析,及协方差分析。
单因素方差分析
单因素方差分析研究一个控制变量是否对观测变量产生了显著影响, 即检验控制变量不同水平下的观测变量均值的差异。其实质是多个总体的均值是否相同的假设检验,原假设为所有总体的均值都相同,即有\(\mu_1 = \mu_2 = ... = \mu_5\)。
单因素方差分析将观测样本总的离差平方和\(S_T\)分解为组间离差平方和\(S_A\)以及组内离差平方和\(S_E\)两部分,即:
\[ S_T = S_A + S_E \]
用\(S_A\)(服从\(\chi^2\)分布)与所有\(S_E\)(服从\(\chi^2\)分布)的比值(服从\(F\)分布)为统计量,来判断控制变量对观测值的影响。其中有\(S_T\):
\[ \mathrm { S } _ { \mathrm { T } } = \sum _ { \mathrm { i } = 1 } ^ { \mathrm { s } } \sum _ { j = 1 } ^ { n _ { i } } \left( x _ { i j } - \bar { x } \right) ^ { 2 } \quad \bar { x } = \frac { 1 } { n } \sum _ { i = 1 } ^ { s } \sum _ { j = 1 } ^ { n _ { i } } x _ { i j } \]
其中\(s\)为控制变量总类别数,\(n_i\)为在控制变量水平为\(i\)的情况下观测变量的例数。\(\bar x\)为所有观测变量的均值。同理,有\(S_A\)为:
\[ \mathrm { S } _ { A } = \sum _ { i = 1 } ^ { s } \sum _ { j = 1 } ^ { n _ { i } } \left( \bar { x } _ { i } - \bar { x } \right) ^ { 2 } = \sum _ { i = 1 } ^ { s } n _ { i } \left( \bar { x } _ { i } - \bar { x } \right) ^ { 2 } \]
其中\(x_i\)为在控制变量水平为\(i\)的情况下观测变量的均值。\(S_A\)为各水平组均值与总均值离差的平方和。反映的是控制变量不同水平对观测变量带来的影响。同有\(S_E\):
\[ S _ { E } = \sum _ { i = 1 } ^ { s } \sum _ { j = 1 } ^ { n _ { i } } \left( x _ { i j } - \bar { x } _ { i } \right) ^ { 2 } \]
\(S_E\)是每个样本数据与本水平组均值离差的平方和,反映了抽样误差。最终计算的统计量为:
\[ f = \frac { S _ { A } / ( s - 1 ) } { S _ { E } / ( n - s ) } \sim F ( s - 1 , n - s ) \]
可见,如果\(f\)较大,则观测变量的变动主要由控制变量引起,可由控制变量解释。反之,控制变量没有对观测变量带来影响,观测变量的变动主要由随机变量引起。若统计量\(f > f_a(s-1, n-s)\),则表明\(S_A\)较大,以\(a\)的概率拒绝原假设,即控制变量对观测变量有显著影响。反之,接受\(H_0\),该控制变量对观测变量的影响不显著。
在用SPSS进行单因素方差分析之前,通常需要用箱线图大概观察下控制变量各分组下观测变量的水平。然后使用K-S检验并结合P-P图等手段判断各分组下观测变量的值是否符合正态分布(可以使用分析-描述统计-探索填入因变量和因子之后在绘制中选择带检验的正态图来进行分组正态性检验;可以结合数据-拆分文件对数据进行拆分后使用单样本t检验进行)。进行方差分析可以用分析-比较均值-单因素ANOVA,一般需要先比较方差齐性,如果满足方差齐性且各分组符合正态分布则可以使用单因素方差的结果。如果不满足方差齐性,则可以使用Brown-Forsythe检验或者Welch检验的值(在选项中可以勾选)。当然,如果无法确保各总体的为正态分布,或数据量比较小,可以尝试非参数方法。
多重比较
单因素方差分析的基本分析只能判断控制变量(自变量)是否对观测变量(因变量)产生了显著影响。若产生了影响,还需进一步确定,控制变量的不同水平对观测变量影响程度如何,即哪个水平的作用明显不同于其他水平,哪个水平的作用是不显著。
当然,控制变量不同水平下观测变量总体方差无显著差异是方差分析的前提要求,如果不能满足方差齐次,就不能认为各总体分布相同。进行逐对多重检验时要进行方差齐次检验。
多重比较利用全部观测变量值,实现对各个水平下观测变量总体均值的逐对比较。虽然各种比较方法的统计量不同,但是其原假设都是相应水平下观测变量的均值间不存在显著差异。
多重比较方法简述
方差齐性时:
LSD方法:其特点为检验敏感性高,即水平间的均值只要存在一定程度的微小差异就能够被检验出来。统计量为t统计量,适用于各总体方差相等的情况。
Tukey方法:采用了q统计量,仅适用于各水平下观测值个数相等的条件。也要求各总体方差相等。可以用来划分相似性子集。划分子集通常可以根据显著性从高到低排列优先级进行。
S-N-K方法:一种有效划分相似性子集的方法,也像Tukey法一样适合于各水平观测值个数相等的情况。比Tukey法灵敏,但不如LSD灵敏。
Scheffe法:采用了S统计量,与Tukey方法比,不十分敏感。
方差不齐时:
- Tamhane's T2:在方差不相同的前提下进行的两独立样本的t检验
通常在进行单因素方差分析时会同时进行方差齐性检验,从而判断在多重比较时信任哪一个统计量得出的结果。
多重比较可以通过单因素方差分析中的两两比较选项内进行选择。通常可以结合选项里面的方差同质性检验与均值图一起使用。
趋势检验
当控制变量(自变量)为定序变量时,趋势检验能够分析随着控制变量水平的变化,观测变量值变化的趋势,是呈线性变化趋势,还是二次,三次等多项式变化。通过趋势检验,从另一角度把握控制变量不同水平对观测变量总体作用的程度。
趋势检验可以通过对比窗口进行。结果如图所示。
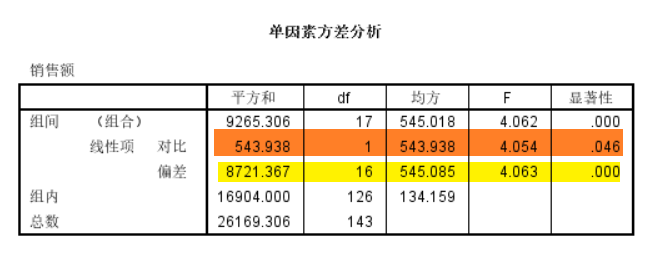
勾选多项式后可以选择衡量线性还是高次方关系。趋势检验将组间差进一步细分为可被自变量线性解释的变差(橙色部分)和不能被自变量线性关系解释的变差(黄色部分)。根据显著性(橙色部分Sig值)可以判断随着控制变量水平的变化,观测变量值是否呈线性变化趋势。如果显著性值小于0.05,则通常认为存在线性相关趋势。
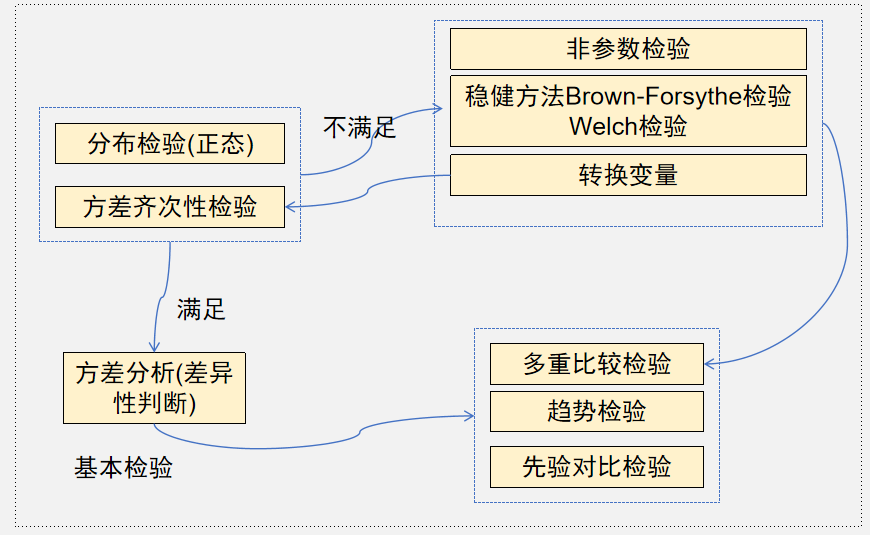
总体流程
进行单因素方差分析的总体流程如下图: