协方差分析
在许多实际问题中,有些控制因素往往很难人为控制,但他们确会对观察变量产生较为显著地影响。在方差分析中,如果忽略这些因素的存在而单纯去分析其他因素对观测变量的影响,往往会夸大或缩小其他因素的影响作用,使分析结论不准确。
为了更加准确地研究控制变量对观测变量影响,应尽量排除其他可能因素对分析结论的影响。协方差分析将某些难以人为控制的因素作为协变量,在排除协变量对观测变量的影响条件下,分析控制变量对观测变量的作用,从而更加准确地对控制因素进行评价。
协方差分析基本思想
基本思想:观测变量的变动受四个方面的影响
- 控制变量独立的影响
- 控制变量的交互作用
- 协变量作用
- 随机因素的作用
协方差分析扣除协变量的影响后,再分析控制变量对观测变量的影响。
协方差分析的假设与模型
协方差分析的原假设是协变量对观测变量的线性影响不显著的。其通过F统计量来判断,F大,则说明协变量是引起观测变量变化的因素之一,观测变量的变动可以部分地由协变量来线性解释。反之,协变量对观测变量变化无影响。
单因素协方差的数学模型如下:
\[ x_{ij} = \mu + \alpha_i + \beta z_{ij}+ \varepsilon_{ij} \]
其中\(x_{ij}\)是水平\(A_i\)下第\(j\)次试验的因变量的观察值;\(\mu\)为因变量的理论值,\(\alpha_i\)为控制变量水平\(A_i\)对实验结果产生的影响。\(z_{ij}\)为水平\(A_i\)下第\(j\)次实验的样本对应的协变量的值;\(\beta\)为回归系数,\(\varepsilon_{ij}\)为随机误差。
在协方差分析中,协变量一般是连续变量。其中,因变量和协变量之间有显著的线性关系(研究假设)。同时,协方差分析中要求协变量与控制变量不存在交互作用,即协变量与控制变量相互独立,满足回归的同质性假设。
回归同质性假设
回归同质性假设说明了协变量与因变量的关联性在控制变量的各水平组内是相同的,对于回归同质性假设检验是执行协方差分析的必要工作。
SPSS中的协方差分析前的准备
在进行协方差分析之前需要做好两个准备:检验协变量与因变量之间的线性关系,以及判断数据是否符合回归同质性假设。
检验因变量与协变量之间的线性关系时,需要在控制变量的同一水平内进行。可以按照控制变量拆分数据集,并分组进行相关分析,也可以画图,通过图形-图表构建程序中的分组散点图,将因变量和协变量分别作为x,y轴,将控制变量作为分组依据画图。例子入下图所示。
画好图后,可以在输出报告中右键单击图,选择编辑内容-在单独窗口中,通过点击上方的添加子组拟合线为图上各组散点图添加拟合线。如下图所示。
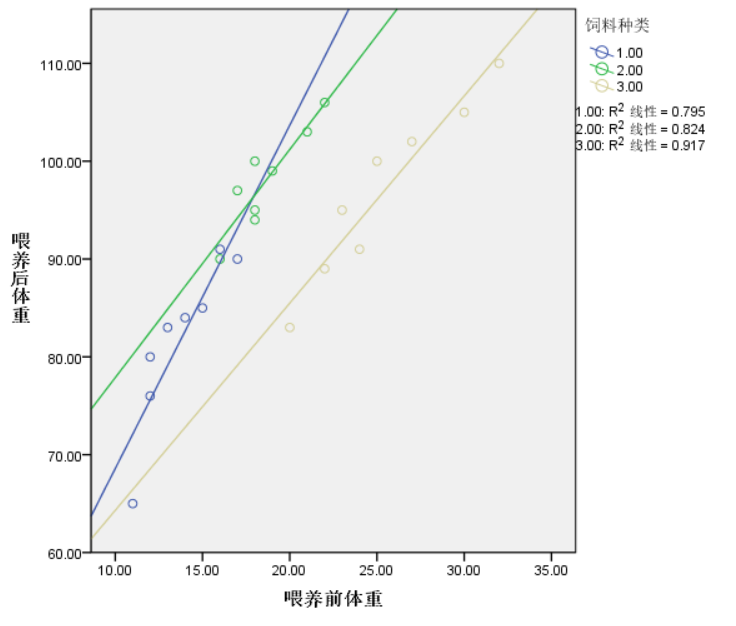
假如在控制变量的不同水平下,协变量与因变量都存在较强的线性关系,且各个分组拟合直线的斜率都基本相同的话,可以认为协变量与因变量之间存在线性关系,且初步认为数据符合回归同质性假设。
进行回归同质性假设,可以使用分析-一般线性模型-单变量进行检验。分别将因变量,控制变量以及协变量填入对应选框中,再点击右上角模型按钮,在新页面中的指定模型处点击设定,并将控制变量、协变量以及他们的交互作用填入模型中。在生成的报告中我们可以观察交互效应的Sig值。如果Sig值大于0.05,则可以认为各水平上的协变量和自变量不存在交互作用。
进行上述检测后才能进行协方差分析。
SPSS中的协方差分析
同样使用分析-一般线性模型-单变量进行检验。将模型中的交互项移除,仅使用控制变量与协变量进行分析即可。
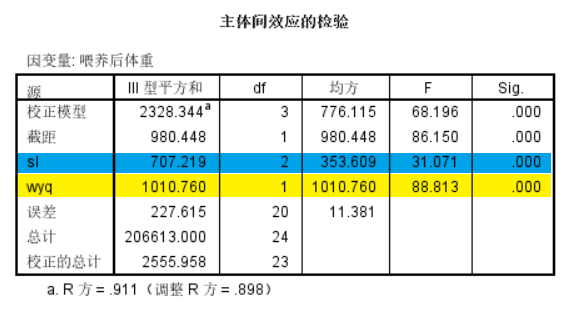
sl代表饲料,为控制变量,wyq代表喂养前体重,为协变量,因变量为喂养后体重。从报告图中可以看出,协变量对应的F = 88.813,p = 0.000,这说明协变量(生猪的体重)与 观测变量(生猪的体重增长)之间存在可解释的线性关系。即喂养前生猪的体重对生猪体重增加有显著影响,同样在排除了喂养前体重的影响下,不同饲料对生猪体重的增加也存在显著差异(F=57.987,p=0.0)。
我们可以将协方差分析的结果与不考虑协变量的单因素方差分析结果进行对比。
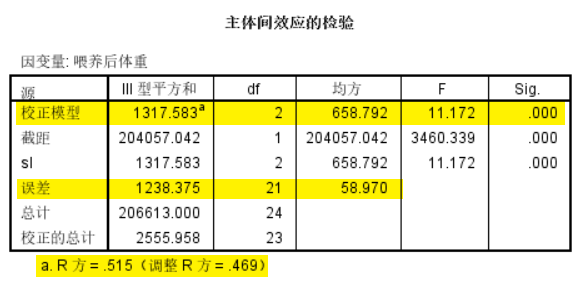
可以看出,相比于不考虑协变量的单因素方差分析结果,协方差分析中模型的随机误差从1238.375减少到227.615,模型的调整后的R方从0.469上升到了0.898,证明将喂养前体重作为协变量引入模型是非常正确的选择,能够大幅提高模型的拟合优度。同时,饲料的可解释变差由1317.583减小为707.219,这是由于扣除了喂养前体重的影响造成的。
在分析-一般线性模型-单变量点击绘制,我们可以绘制在不同控制变量水平下因变量的均值差异。在不考虑协变量的单因素方差分析结果中,通过将控制变量sl(饲料)添加入水平轴,我们可以绘制均值图如下:
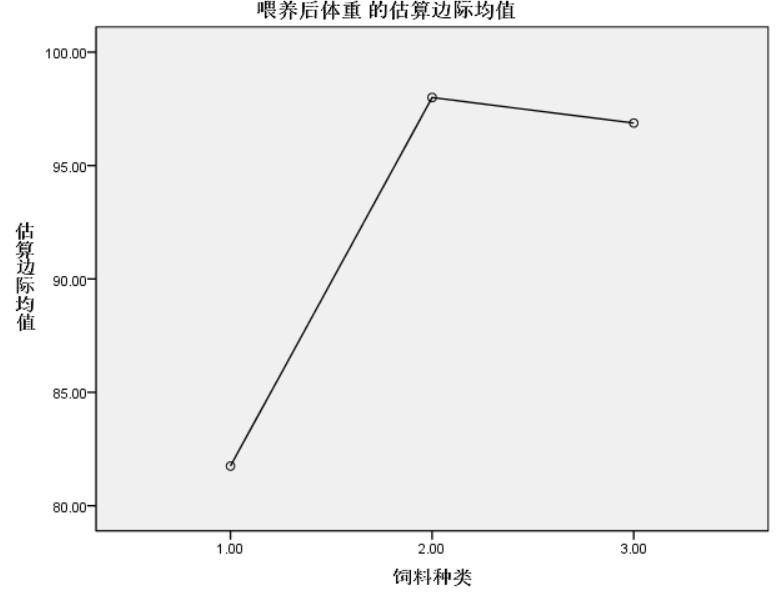
根据均值排序,最好饲料2,最差饲料1,饲料3与饲料2差距较小。效果排名2-3-1。
在考虑了协变量的协方差分析的结果中,可以通过上述一样的步骤获得均值图如下:
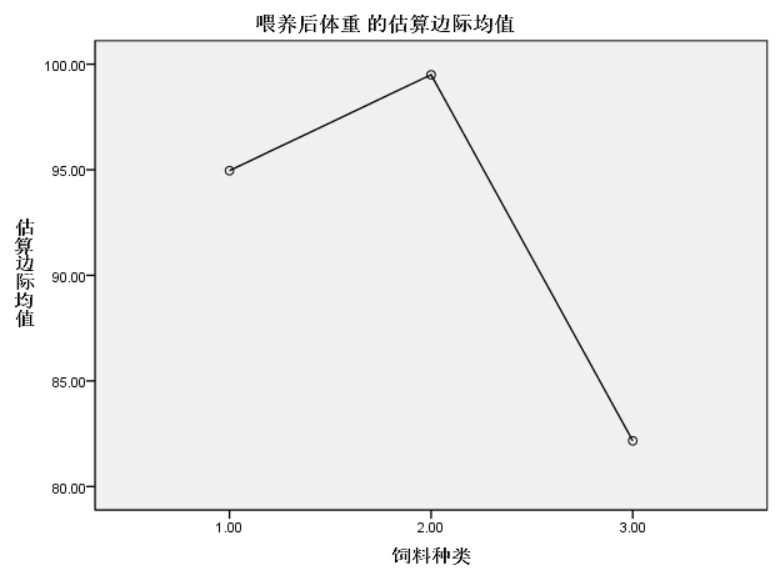
在排除生猪自身体重条件后,饲料的优劣排名为2-1-3。可见,排除协变量影响后的分析结果并不等同于前面的分析。通过绘制喂养前体重与饲料种类的分组箱线图可以看出,第三组生猪喂养前的体重明显高于第一组,因此第三组生猪增重的幅度本来就比第一组生猪的幅度要更大。
协方差分析总结
核心目的:需要尽力排除非控制因素的干扰和影响,从而准确地获得控制因素的实验效应。
方法:在做两组或多组均数间的比较前,用直线回归找出各组因变量Y和协变量X之间的数量关系,求得假定X相等时的修正均值,再利用方差分析比较修正均值之间的差别。该方法是定量分析中控制混杂因素的重要手段之一。
